Максимальное и минимальное количество узлов в дереве суффиксов

Question

Каково максимальное и минимальное количество узлов в дереве суффиксов? И как я могу это доказать?

Answer 1

Предполагая ввод текста N длина символов, минимальное количество узлов, включая корневой узел и все конечные узлы, составляет N+1максимальное количество узлов, включая корень и листья, 2N-1,

Доказательство минимума: должен быть хотя бы один листовой узел для каждого суффикса, и есть N суффиксы. Не должно быть никаких внутренних узлов, например: если текст представляет собой последовательность уникальных символов, abc$, нет никаких ветвей, следовательно нет внутренних узлов в результирующем дереве суффиксов:

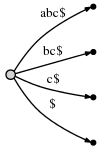
Следовательно, минимум N листья, 0 внутренние узлы и 1 корневой узел, в сумме N+1 узлы.

Доказательство максимума: число листовых узлов никогда не может быть больше Nпотому что конечный узел - это место, где заканчивается суффикс, и вы не можете иметь больше, чем N различные суффиксы в строке длины N, (На самом деле, у вас всегда есть точно N различные суффиксы, следовательно N листовые узлы точно.) Корневой узел всегда точно 1, поэтому вопрос в том, каково максимальное количество внутренних узлов. Каждый внутренний узел вводит ветвь в дереве (поскольку внутренние узлы дерева суффиксов имеют как минимум 2 дочерних элемента). Каждая новая ветвь должна в конечном итоге привести как минимум к одному дополнительному листовому узлу, так что если у вас есть K внутренних узлов, должно быть не менее K+1 листовые узлы, а наличие корневого узла требует как минимум одного дополнительного листа (если дерево не пустое). Но количество листовых узлов ограничено N, поэтому максимальное количество внутренних узлов ограничено N-2, Это дает точно N листья, 1 корень, и максимум N-2 внутренние узлы, 2N-1 в целом.

Чтобы увидеть, что это не только теоретическая верхняя граница, но некоторые деревья суффиксов фактически достигают этого максимума, рассмотрим в качестве примера строку с одним повторяющимся символом: "aaa$". Убедитесь, что дерево суффиксов для этого имеет 7 узлов (включая корень и листья):

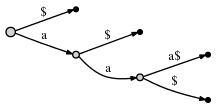
Резюме: как видно, единственной реальной переменной является количество внутренних узлов; количество корней и листьев постоянно 1 а также N для всех деревьев суффиксов, в то время как число внутренних узлов варьируется между 0 а также N-2,