Нахождение "направления движения" (угла) точки

Question

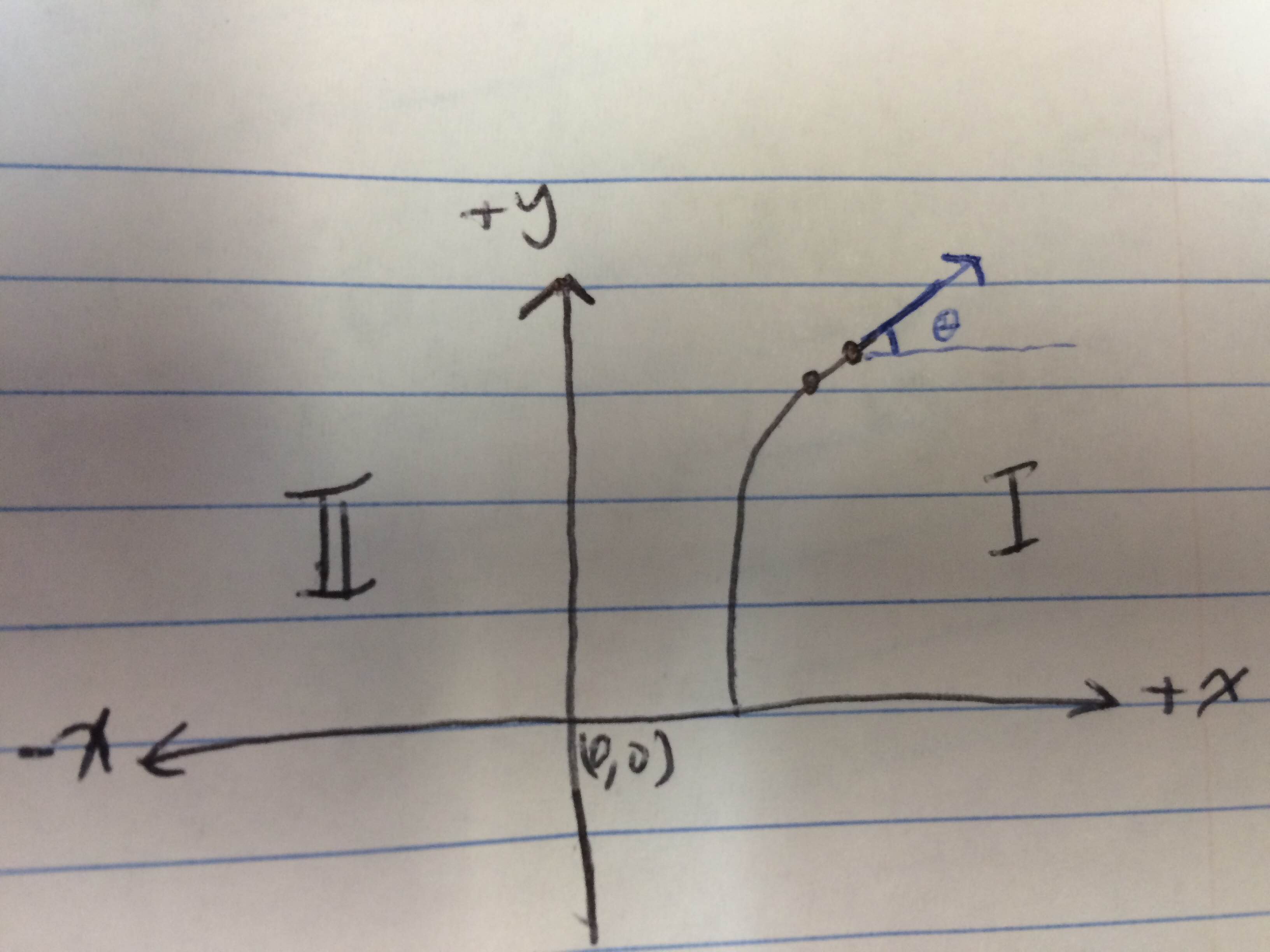
Я работаю над довольно классным проектом, в котором я собираю данные о движении курсора, но столкнулся с проблемой, в которой, как мне кажется, я мог бы использовать некоторую помощь. Я постоянно читаю данные о положении курсора по осям x и y (вместе с другими соответствующими данными), и как только курсор превысит определенный порог в измерении y, мне нужно рассчитать направление движения (угол). Позвольте мне проиллюстрировать рисунок, который я нарисовал:

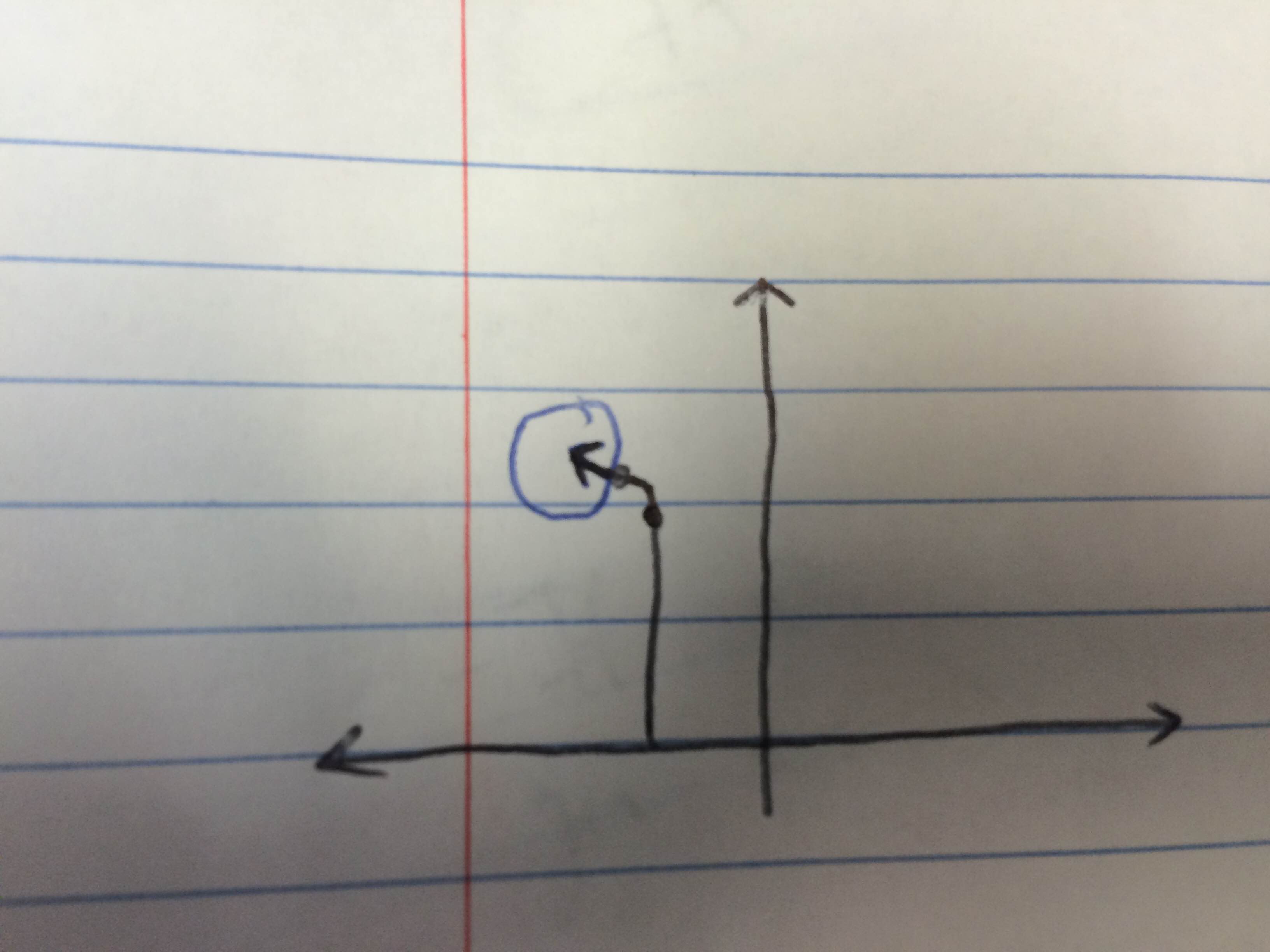
Обычно происходит то, что курсор перемещается по несколько прямой линии, но затем изгибается к концу движения. Мне нужно рассчитать тета, т. Е. Угол синего вектора относительно положительной оси х. Идея, которую я придумал, состоит в том, чтобы использовать последние 2 сэмпла, чтобы в значительной степени определить направление движения, в противном случае, если я использую слишком много сэмплов, я искажу фактический угол. Чтобы привести крайний случай, позвольте мне привести еще одну картину:

Здесь каждая точка представляет образец. Обратите внимание, что если я использую ОБА точки, нужный угол будет неправильным (опять же, мне нужно найти направление, в котором курсор двигался в последний раз, то есть вектор, нарисованный в конце линии). Я не ожидаю, что этот случай выйдет много, но мне было интересно, найдется ли способ решить его, если это произойдет.

Наконец, обратите внимание, что эти движения могут происходить как в первом, так и во втором квадранте, если это имеет значение.

Я бы очень признателен за любую помощь здесь. Я пишу это на C++, но думаю, что смогу перевести любой ответ. Благодарю.

Answer 1

Это должно помочь вам начать http://jsfiddle.net/0ao9oa7a/

• Получите все записанные очки
• Отфильтровать точки, которые находятся близко друг к другу (я использую 5 пикселей)
• Найти углы каждой последовательной пары точек (atan2)
• Найти абсолютные различия между каждой последовательной парой углов
• • Выбросьте все углы до максимальной разницы
• Усредните оставшиеся углы (усредните все точечные векторы, затем atan2 обратно в угол)

Код

function process(points) {
    if(points.length === 0) { 
        txt = "Not enough points\n" + txt;
        return null; 
    }
    // compress points, removing those that are too close together
    var newPoints = [];
    newPoints.push(points[0]);
    for(var i = 1; i < points.length; i++) {
        if(Math.sqrt(Math.pow(points[i].x - newPoints[newPoints.length - 1].x, 2) + Math.pow(points[i].y - newPoints[newPoints.length - 1].y, 2)) > 5) {
            newPoints.push(points[i]);
        }
    }
    points = newPoints;
    if(points.length < 2) { 
        txt = "Not enough points\n" + txt;
        return null; 
    }
    // get all of the angles
    var angles = [];
    for(var i=0; i < points.length - 1; i++) {
        var rad = Math.atan2(points[i + 1].y - points[i].y, points[i + 1].x - points[i].x);
        angles[i] = rad;
        txt += "x: " + (points[i].x|0) + " y: " + (points[i].y|0) + " x: " + (points[i+1].x|0) + " y: " + (points[i+1].y|0) + " [" + ((rad * 180 / Math.PI)|0) + "]" + "\n";
    }
    txt += "\n";
    // get all of the diffs between angles
    // save the index of the max diff
    var absDiffs = [];
    var maxDiff = -1;
    var maxDiffAngleIndex = -1;
    for(var i=0; i < points.length - 1; i++) {
        var delta = Math.abs(angles[i] - angles[i + 1]);
        if(delta >= maxDiff) {
            maxDiff = delta;
            maxDiffAngleIndex = i + 1;
        }
    }
    if(maxDiffAngleIndex == -1) {
        txt = "Angle: " + angles[0] + " : " + (angles[0] * 180 / Math.PI) + "\n" + txt;
        return angles[0];
    } else if(maxDiffAngleIndex == angles.length - 1) {
        txt = "Angle: " + angles[angle.length - 1] + " : " + (angles[angles.length - 1] * 180 / Math.PI) + "\n" + txt;
        return angles[angles.length - 1];
    } else {
        // find the average angle from the index to the end
        var sumX = 0;
        var sumY = 0;
        for(var i = maxDiffAngleIndex; i < angles.length; i++) {
            sumX += Math.cos(angles[i]);
            sumY += Math.sin(angles[i]);
        }
        var avgX = sumX / (angles.length - maxDiffAngleIndex);
        var avgY = sumY / (angles.length - maxDiffAngleIndex);
        //
        var avgAngle = Math.atan2(avgY, avgX);
        txt = "Angle: " + avgAngle + " : " + (avgAngle * 180 / Math.PI) + "\n" + txt;
        return avgAngle;
    }
}

Answer 2

Как я вижу, "направление движения" (угол) точки будет угловым коэффициентом двух точек: одна точка в конце вектора, а другая - в начале.

Потому что мы можем найти угол только с двумя точками, поэтому мы можем сделать линию, так как вектор направления будет (B-A), где A а также B те моменты, о которых я уже говорил

Мы можем рассчитать это по формуле углового коэффициента линии:

m = Tan θ = Δy / Δx

И это просто:

Tan θ = (yB - yA) / (xB - xA)

Где θ - это "направление движения" (угол), а (x,y) - координаты точек A и B.

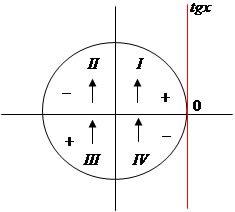
Говоря о квадранте, вам нужно будет использовать только тригонометрический круг, чтобы узнать синал значения Tan θ, поэтому взгляните на это изображение:

И, конечно же, после того, как вы найдете значение Tan θ, вам нужно будет использовать его, чтобы найти arctan θи это будет ваш окончательный ответ.