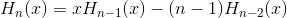Реализация полиномов Хаскелла Эрмита

Question

Haskell позволяет представлять рекуррентные функции очень лаконично. Например, бесконечный список, содержащий числа Фибоначчи, может быть определен следующим образом:

fibs :: [Integer]
fibs = 1 : 1 : zipWith (+) fibs (tail fibs)

Я имею дело с полиномами Эрмита "вероятностников", которые имеют следующее отношение рекурсии:

Каков был бы оптимальный способ построения бесконечного списка n-й полиномов Эрмита для заданного x?

Answer 1

Мы можем написать это как:

hermite :: (Enum n, Num n) => n -> [n]
hermite x = s
    where s@(_:ts) = 1 : x : zipWith3 (\hn2 hn1 n1 -> x*hn1 - n1*hn2) s ts [1..]

где первые предметы 1 : x : ... являются первыми элементами hermite (вы можете заполнить другие значения).

Для следующего мы заархивируем исходные значения s (так что начинается с H0), хвост ts из s (это начинается с H1) и индекс (который начинается с 2, 3,...) и выполнить операцию x*hn1 - x*hn2 (nh1 обозначает Н_н-1, и nh2 обозначает H_n-2), и поэтому мы вычисляем следующий элемент каждый раз.

Первые 11 значений для x = 0.75 являются:

Prelude> take 11 (hermite 0.75)
[1.0,0.75,-0.4375,-1.828125,-5.859375e-2,7.2685546875,5.744384765625,-39.30303955078125,-69.68797302246094,262.1583366394043,823.8105096817017]

Итак, первое значение равно 1, второе x, третий x*x-2четвертый x*x*x-2*x-3*x, и так далее.

При этом, если я правильно помню, формула рекурсии полиномов Эрмита:

H_n(x) = 2 × x × H_n-1(x) -2 × (n-1) H_n-2(x)

вместо того, который указан в вопросе.

В этом случае формула такова:

hermite :: (Enum n, Num n) => n -> [n]
hermite x = s
    where s@(_:ts) = 1 : 2 * x : zipWith3 helper s ts [1..]
          helper hn2 hn1 n1 = 2 * (x * hn1 - n1 * hn2)

Тогда первые 11 значений:

Prelude> take 11 (hermite 0.75)
[1.0,1.5,0.25,-5.625,-9.9375,30.09375,144.515625,-144.3515625,-2239.74609375,-1049.994140625,38740.4384765625]

Что является правильным согласно этой статье Wolfram:

H₀ = 1

H₁ = 2 * x

H₂ = 4 ײ - 2

H₃ = 8 ׳ - 4 ×

H₄ = 16 ×⁴ - 48 ײ + 12

Какие карты точно соответствуют значениям, которые мы получили:

Prelude> let x = 0.75 in [1,2*x,4*x*x-2,8*x*x*x-4*x,16*x*x*x*x-48*x*x+12]
[1.0,1.5,0.25,0.375,-9.9375]