Правильное построение большой матрицы смежности в R
У меня есть довольно большая (но довольно редкая) матрица смежности (500x500), которую я пытаюсь визуально представить. Мне кажется, что что-то похожее на силовой ориентированный граф - моя лучшая ставка, и, пытаясь найти лучший способ реализовать это, я натолкнулся на более чем один ресурс для R. Самым полезным для этого была сетевая визуализация на http://kateto.net/network-visualization Хотя я никогда раньше не использовал R, похоже, у него много полезных функций для такого рода визуализации.
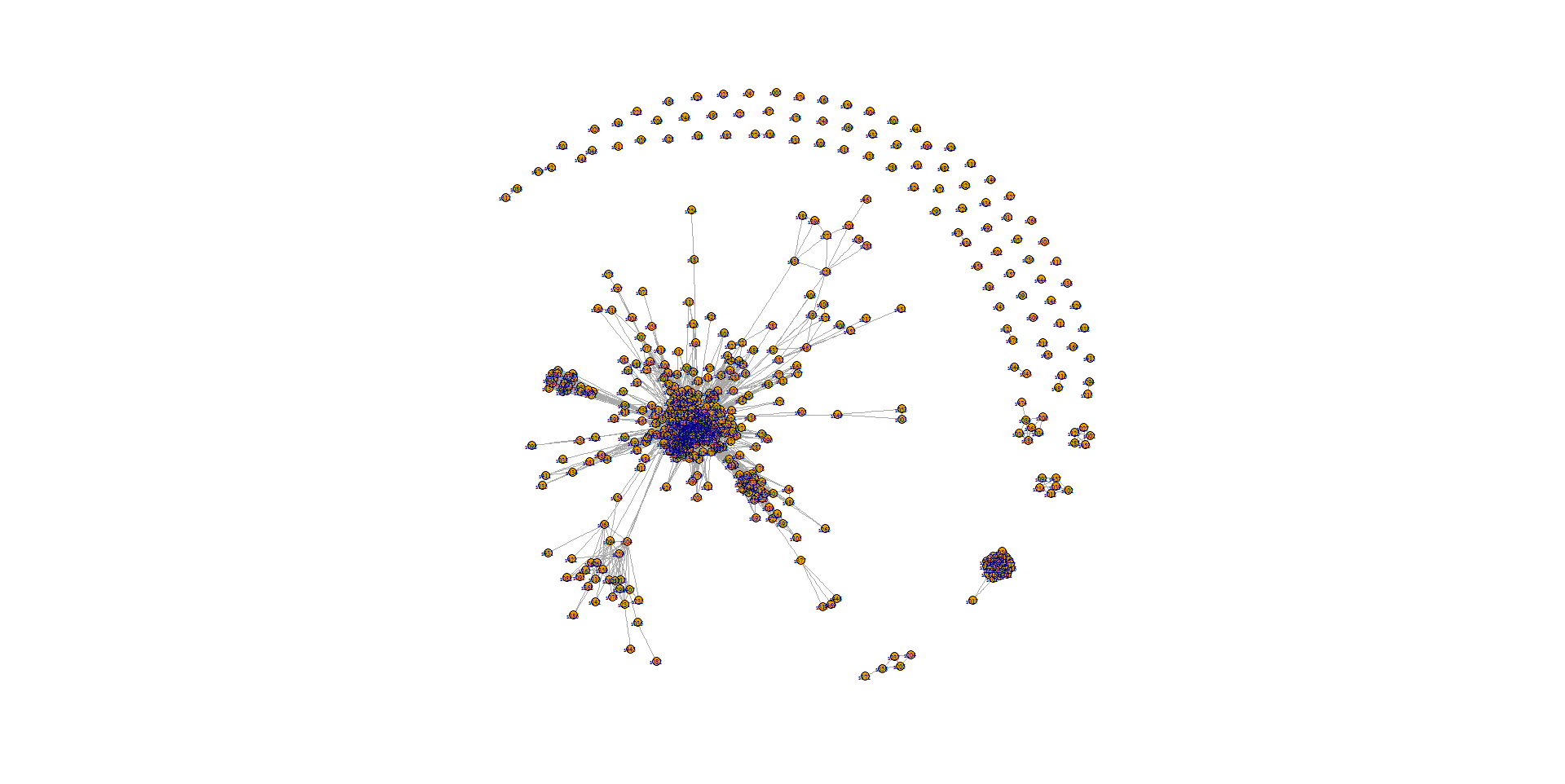
Мне удалось создать график ниже, но изображение довольно маленькое, а узлы сложены.
Разрешение немного лучше, если я печатаю в pdf, а не в формате PNG, но у меня все еще есть проблема с укладкой. Поэтому мой вопрос: как правильно построить большую матрицу смежности в R для решения этих проблем?
На данный момент мой код выглядит следующим образом (с помощью нескольких последних строк я попытался представить данные несколькими разными способами). Любые советы с благодарностью. Заранее спасибо.
Для удобства я загрузил два файла, на которые ссылается мой GitHub, здесь https://github.com/BStricklin/DataViz.
plot.new()
library('igraph')
setwd("D:/Downloads/polnet2016/Data files")
nodes2 <- read.csv("nodes.csv", header=T, as.is=T)
links2 <- read.csv("nodeAdjacency.csv", header=T, row.names=1)
links2 <- as.matrix(links2)
head(nodes2)
head(links2)
net2 <- graph_from_incidence_matrix(links2)
net2 <- graph_from_adjacency_matrix(links2, mode = "undirected", weighted = TRUE)
net2 <- simplify(net2, remove.multiple = F, remove.loops = T)
V(net2)$label <- nodes2$id
deg <- degree(net2, mode="all")
V(net2)$size <- deg*3
#plot(net2)
#plot(net2, edge.label=round(E(net2)$weight, 3))
layout <- layout.reingold.tilford(net2)
#plot.igraph(net2,vertex.size=3,layout=layout.lgl)
plot.igraph(net2,vertex.size=3,vertex.label.cex=.5,layout=layout.fruchterman.reingold(net2, niter=10000))
РЕДАКТИРОВАТЬ: Для тех, кто интересуется, как я закончил делать это, я должен был использовать MATLAB и использовать функции графика и графика. Это выглядело так же противно, как изображение R, но с некоторой настройкой узлов и использованием функции масштабирования это работало достаточно хорошо. Мне все равно было бы интересно, как это сделать в R, хотя.
2 ответа
Одна вещь, с которой вы могли бы начать, чтобы упростить визуализацию сети, - это удалить несвязанные вершины - те, у которых степень меньше 1:
net3 <- delete.vertices(net2, degree(net2)<1)
Затем вы можете использовать алгоритм макета, более подходящий для больших сетей, например layout_with_graphopt, алгоритм, ориентированный на усилие, который позволяет установить начальную длину "пружин", которые создают силы, которые в конечном итоге приведут к окончательной компоновке:
net.graphopt <- layout_with_graphopt(net3, charge = 0.009, mass = 50, spring.length = E(net3)$weight)
В конце концов, вы можете построить сеть на большей площади (как было предложено выше в первом ответе), увеличивая высоту и ширину pdf() команда, как показано ниже:
pdf("graphopt.pdf", height = 14, width = 14)
plot.igraph(net3,vertex.size=2,vertex.label.cex=.5,layout=net.graphopt)
dev.off()
Конечный результат все еще немного запутан, но, по крайней мере, он позволяет избежать слишком большого перекрытия узлов:
Сеть построена с использованием igraph::layout_with_graphopt
Попробуйте увеличить площадь участка:
png("network_name.png", width = 15, height = 15, units = "in", res = 300)
plot.igraph(net2,vertex.size=3,
vertex.label.cex=.5,
layout=layout.fruchterman.reingold(net2, niter=10000))
dev.off()
Если вы стремитесь придерживаться представления в виде сети, необходимо оптимизировать параметры макета алгоритма макета графа, в вашем случае те, что в вашем случае - Fruchterman-Reingold, чтобы получить симпатичный макет.
Альтернативным решением было бы использование другого представления в качестве простой матрицы, см. " Графики смежных матриц с R и ggplot2".
И последнее, но не менее важное: вы можете выбрать самый крупный компонент и нанести его на график отдельно, как я обычно это делаю.