Неожиданные результаты при использовании octaveFilter в Matlab
Я стремлюсь получить частотный сигнал в 1/3 октавной полосы для определенных центральных частот. Я хочу использовать функцию Matlab octaveFilter, но я ожидал получить одиночный пик полосы в 1/3 октавы при 1000 Гц, но вместо этого в крайнем левом и крайнем правом положениях 1000 Гц были вычислены очень положительные уровни звукового давления.
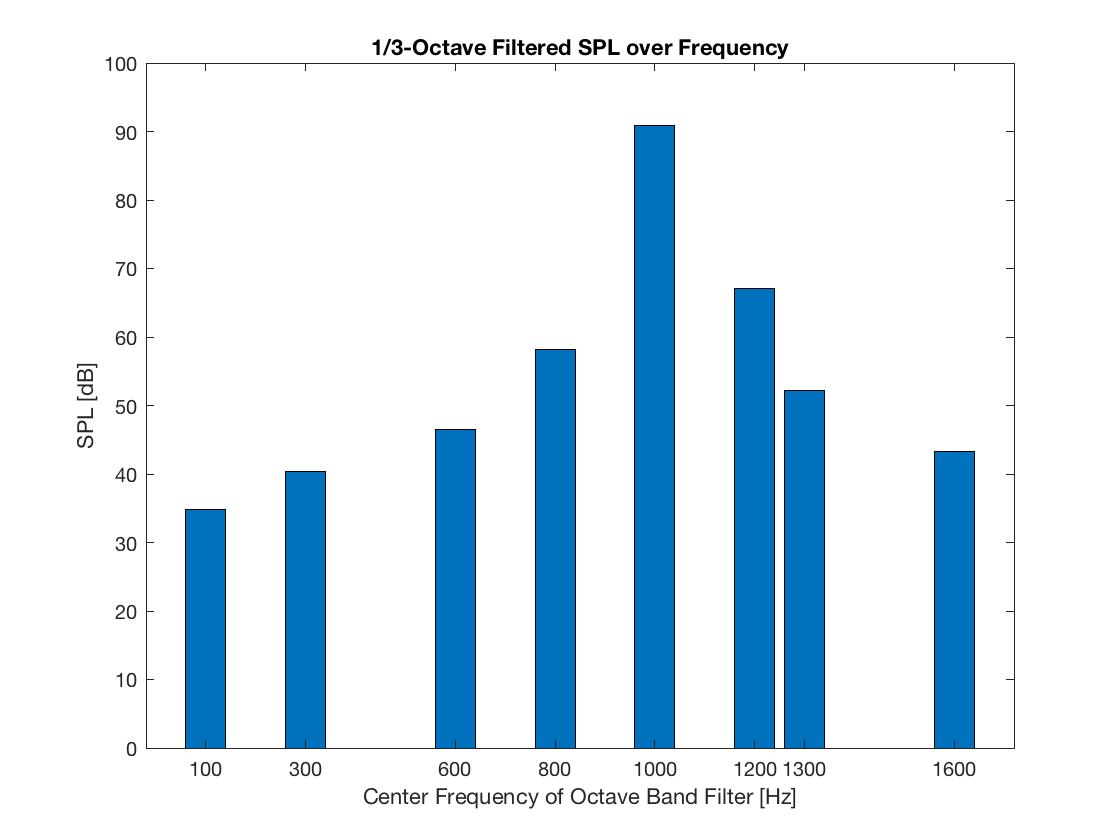
Что я делаю не так?
Fs = 48000; % Sampling rate
t = 0:1/Fs:1-1/Fs; % Time vector of 1 second
f = 1000; % Frequency of signal
dpres = sin(2*pi*f*t); % Signal in [Pa]
frCen = [100 300 600 800 1000 1200 1300 1600];
[Spl,frCen] = CompOctSplFreq(dpres,frCen)
figure()
semilogx(frCen,Spl,'ro-')
title('1/3-Octave Filtered SPL over Frequency')
xlabel('Center Frequency of Octave Band Filter [Hz]')
ylabel('SPL [dB]')
function [Spl,frCen] = CompOctSplFreq(dpres,frCen);
% Reads singal in pressure over time
freqNum = length(frCen);
Fs = length(dpres);
% Setting up the 1/3-octave filters for all center frequencies
for f = 1:freqNum
octaveFilterBank{f} = octaveFilter(frCen(f),'1/3 octave','SampleRate',Fs,'FilterOrder',12);
% Filtering the signal with the corresponding filters
dpresFiltered(:,f) = octaveFilterBank{f}(dpres');
% Getting the average for each filter frequency band
drms(f) = sqrt(sum(dpresFiltered(:,f).^2)/length(dpresFiltered(:,f)));
end
% Converting the root mean square pressure to SPL
pRef = 20e-06; % Reference pressure
Spl = 20*log10(drms/pRef);
end
1 ответ
Основная проблема заключается в том, что вы вычисляете мощность сигналов, которые в некоторых случаях включают значительный переходный отклик. Чтобы проиллюстрировать это, последующее будет проходить через получение ожидаемого отклика в стационарном состоянии и сравнивать полученные в результате вычисленные отклики, включая и исключая переходную часть.
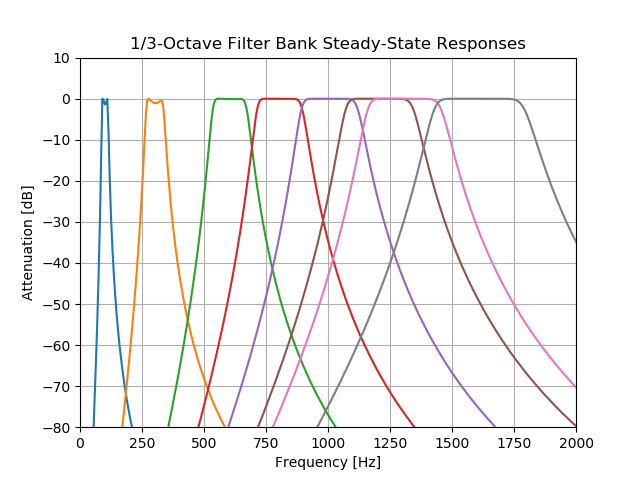
Основываясь на описании алгоритма octaveFilter, можно построить идеальный отклик устойчивого состояния каждого фильтра в вашем банке фильтров. Эти ответы приведены на следующем графике:
Обратите внимание, что ответы значительно выходят за пределы указанной полосы, но они не исчезают полностью. В результате входные сигналы с частотой вне указанной полосы будут по-прежнему вызывать некоторый выход (хотя и небольшой) для всех фильтров в банке фильтров. Для синусоидального входного сигнала на частоте 1000 Гц вы можете получить ответ установившегося состояния на выходе каждого фильтра, посмотрев пересечение соответствующего отклика фильтра вертикальной линией 1000 Гц на приведенном выше графике. Это должно дать вам следующий график отклика блока фильтров на вход 95 дБ на частоте 1000 Гц:
Теперь вы можете заметить, что ваши результаты довольно близки к этим установившимся откликам для фильтров, центрированных около 1000 Гц, но разница увеличивается с удалением от 1000 Гц. Если мы посмотрим на один из отфильтрованных сигналов во временной области, мы можем заметить, что действительно значительная часть энергии может быть найдена во время начального переходного процесса сигнала:
Простое избавление от переходного процесса должно приблизить вас к ожидаемому установившемуся отклику. Самое сложное - выяснить, сколько образцов нужно отбросить. Как общее практическое правило, я обычно использую приблизительно 5 постоянных времени, где одна постоянная времени имеет порядок, обратный половине полосы пропускания фильтра полосы пропускания. Это может быть вычислено с помощью следующего:
G = 10^(3/10);
b = 3; % for 1/3-octave
fhi = frCen(f)*G^(0.5/b);
flow = frCen(f)*G^(-0.5/b);
M = 10/(fhi-flow); % 5 time-constants (one time-constant is ~ 1/((fhi-flow)/2) )
drms(f) = sqrt(sum(dpresFiltered(M:end,f).^2)/length(dpresFiltered(M:end,f)));
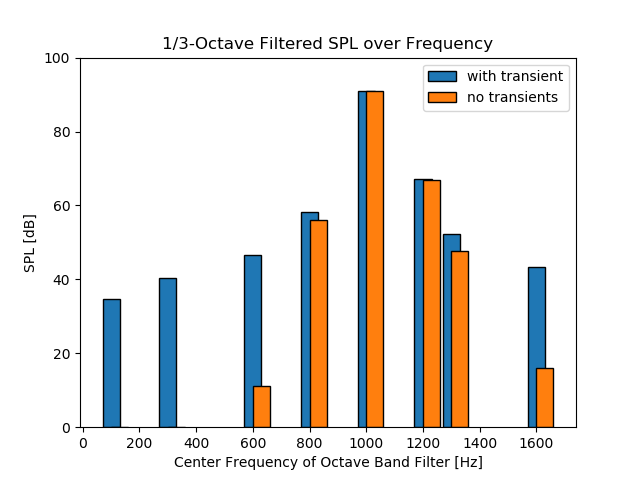
Сравнение результирующего отклика, исключая исходные выборки, соответствующие переходному процессу, с вашими предыдущими результатами, показало бы, что это действительно оказало значительное влияние на график, и что результаты теперь находятся в гораздо лучшем согласии с нашим более ранним идеальным графиком стационарного отклика: