Какое наименьшее де-/ нормализованное число больше 1?(64 бита)

Question

Я борюсь с денормализованными числами.

Я знаю это:

По сути, денормализованный метод с плавающей запятой имеет возможность представлять наименьшее (по величине) число, которое можно представить любым значением с плавающей запятой.

Я также знаю, что числа можно представить так:

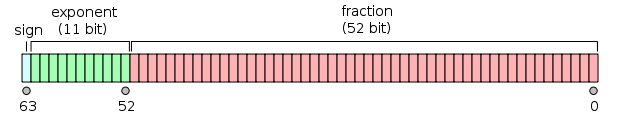
Однако где я застрял - это фактическое вычисление de / нормализованного числа?

Есть ли способ сделать это? Есть ли специальные номера?

Буду признателен за ваш ответ!

Answer 1

"Субнормальный" - это термин, используемый в стандарте IEEE 754.

Субнормальных чисел больше 1 нет; субнормальные числа малы (меньше нормальных чисел).

Минимальный нормальный показатель степени равен -1022 (кодируется как биты 00000000001, так как кодирование показателя степени смещено на 1023). Субнормальные числа имеют более низкую степень кодирования, закодированную как все нулевые биты 00000000000.

Значением субнормального числа является значение и (дробная часть), умноженное на 2^-1022, с примененным знаковым битом (0 для положительного значения, 1 для отрицательного значения). Сигнанда образуется как ведущий 0, затем осевая точка ".", Затем биты значимого и поля. Таким образом, если полезначим содержит 0101010101010101010101010101010101010101010101010101, то значение значится (в двоичном виде) 0,010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101₂.

Если поле значений и равно нулю, значение равно нулю, а число обычно не считается ненормальным. Наименьшее положительное субнормальное число имеет 1 в своем младшем бите и нули во всех остальных битах. Его значение составляет 0,0000000000000000000000000000000000000000000000000001₂• 2^-1022, то есть 2^-52• 2^-1022 = 2^-1074.