Определение областей изображения с "узким местом" с помощью scipy

Question

Я занимаюсь обработкой изображений и математической морфологией с использованием /questions/tagged/scipy.ndimage и действительно наслаждаюсь этим. Наша работа включает в себя моделирование зарядов, движущихся через различные пленки, и мы пытаемся использовать инструменты анализа изображений, чтобы оценить, почему разные морфологии работают лучше, чем другие.

Я быстро смог использовать ndimage.label и distance_transform_edt, чтобы найти подключенные компоненты и определить их размер. Я также реализовал поиск в ширину, чтобы найти минимальные пути между компонентами и краями, которые представляют электроды.

Теперь я бы хотел определить "узкое место" или "узкий канал" регионов. Я даже не уверен, что я ищу правильные ключевые слова, так как мой опыт на самом деле не в обработке изображений. Ниже я привел два примера. Я хочу найти такие элементы, как красные круги, подсчитать их и определить их распределение по размерам. (Учтите, что заряды будут легче проходить через более узкие места.)

Проблема в том, что я не могу маркировать их, так как они не являются независимыми компонентами. Преобразования расстояния дают мне небольшие числа по краям... Я хочу что-то вроде наименьшего расстояния через эти узкие места.

Любой совет, где искать или общие стратегии?

Answer 1

Можно использовать преобразование медиальной оси, чтобы вычислить радиус подгонки шарика в каждой точке набора параметров, чтобы получить уголки на изображении. В следующем примере мы используем водораздел функции расстояния, взвешенной самой функцией расстояния, чтобы получить контуры, которые разделяют минимы (белые компоненты на изображении). Таким образом, это дает путь, взвешенный по максимальному значению функции расстояния, разделяющей 2 белых компонента. Я сделал это в Matlab, но я думаю, что это легко повторить в Scikit.

Изображение1:

Заполнение дыр, поскольку они не являются путями:

Функция расстояния: (тепловая карта)

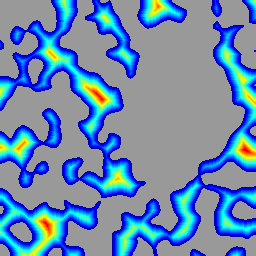
Водораздел дистанционной функции (дорожки):

Водораздел, взвешенный по функции расстояния (конечные пути):

Изображение 2:

Функция расстояния:

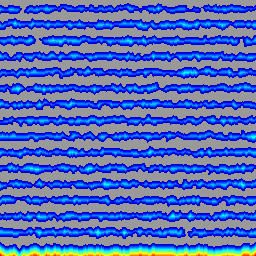
Водораздел дистанционной функции (дорожки):

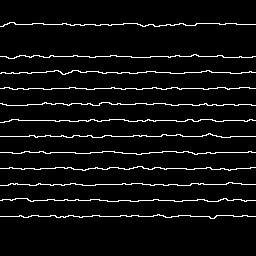
Водораздел, взвешенный по функции расстояния (конечные пути):

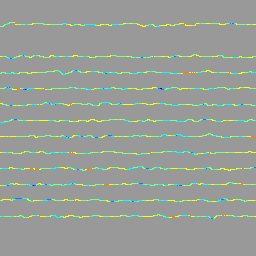
Таким образом, как продемонстрировано, мы вычислили технический каркас по зонам влияния (SKIZ), используя водораздел функции расстояния (здесь использовался городской блок). Следует также отметить, что отверстия на границах не заполнены, так как заполнение игнорирует отверстия на границах. Если его нужно заполнить, можно добавить рамку вокруг, чтобы можно было использовать imfill, чтобы заполнить их позже.