Максимизация усиления на деревьях

Question

Рассмотрим дерево, в котором каждый узел связан с состоянием системы и содержит последовательность действий, которые выполняются в системе.

Корень - это пустой узел, связанный с исходным состоянием системы. Состояние, связанное с узлом n получается путем применения последовательности действий, содержащихся в n в исходное состояние системы. Последовательность действий узла n получается путем помещения нового действия в последовательность действий родителя.

Переход от узла к другому (т. Е. Добавление нового действия к последовательности действий) дает усиление, которое прикрепляется к краю, соединяющему два узла.

Немного "математики":

• каждое состояние системы S связан со значением U(S)
• усиление, достигаемое узлом n связано с государством S не может быть больше чем U(S) и меньше чем 0
• Если n а также m узлы в дереве и n является родителем m, U(n) - U(m) = g(n,m)усиление на границе между n а также m представляет собой уменьшение U от n в m

Смотрите рисунок для примера.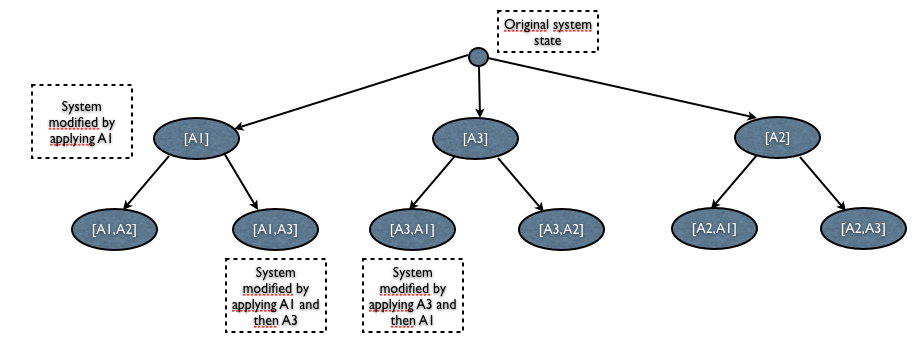

Моя цель - найти путь в дереве, который гарантирует наибольшее усиление (где усиление пути вычисляется путем суммирования всех усилений ребер на пути):

Path* = arg max_{path}  (sum g(n,m), for each adjacent n,m in path)

Обратите внимание, что дерево НЕ известно в начале, и, таким образом, решение, которое не требует посещения всего дерева (отбрасывая те пути, которые наверняка не приводят к оптимальному решению), чтобы найти оптимальное решение, было бы лучшим вариантом.

ПРИМЕЧАНИЕ: я получил ответ здесь и здесь для аналогичной проблемы в автономном режиме, то есть, когда график был известен. Однако в этом контексте дерево не известно, и, таким образом, такие алгоритмы, как Беллман-Форд, будут работать не лучше, чем грубый подход (как предложено). Вместо этого я хотел бы создать что-то, что напоминает возврат, без построения всего дерева, чтобы найти лучшее решение (ветвление и связывание?).

РЕДАКТИРОВАТЬ: U(S) становится все меньше и меньше с увеличением глубины.

Answer 1

Как вы заметили, ветвь и граница могут быть использованы для решения вашей проблемы. Просто расширяйте узлы, которые кажутся наиболее перспективными, пока не найдете полных решений, при этом отслеживая наиболее известные решения. Если узел имеет U(S) ниже, чем самое известное решение во время процесса, просто пропустите его. Когда у вас больше нет узла, все готово.

Вот алгоритм:

pending_nodes <- (root)
best_solution <- nothing

while pending_nodes is not empty
    Drop the node n from pending_nodes having the highest U(n) + gain(n)

    if n is a leaf
        if best_solution = nothing
            best_solution <- n
        else if gain( best_solution ) < gain( n )
            best_solution <- n
        end if
    else
        if best_solution ≠ nothing
            if U(n) + gain(n) < gain(best_solution)
                stop. best_solution is the best
            end if
        end if

        append the children of n to pending_nodes
    end if
end while