Сортировка сетей - какие сети позволяют пропустить сравнение?

Question

GCC реализация qsort использует медиану-3, чтобы выбрать точку разворота. При этом 3 элемента отсортированы с помощью сортировочной сети.

Сортировочная сеть для 3 элементов обычно требует 3 сравнений. Но в этой конкретной реализации последнее сравнение можно пропустить, в зависимости от сравнения:

if(a[0] > a[1]) swap(a[0], a[1]);
if(a[1] > a[2]) swap(a[1], a[2]);
else goto jump;
if(a[0] > a[1]) swap(a[0], a[1]);
jump:;

Можно ли сделать нечто подобное для сетей с n = 4...16 (те, которые имеют минимально известное оптимальное количество сравнений)? Если да, то какие и на что они будут похожи?

ОБНОВЛЕНИЕ: До сих пор я нашел еще одну сеть, которая позволяет пропустить одно сравнение:

// sorting network for 5 elements
if (a[0] > a[1]) { SWAP(a[0], a[1]); }
if (a[2] > a[3]) { SWAP(a[2], a[3]); }

if (a[1] > a[3]) { SWAP(a[1], a[3]); }
if (a[2] > a[4]) { SWAP(a[2], a[4]); }

if (a[0] > a[2]) { SWAP(a[0], a[2]); }
if (a[1] > a[4]) { SWAP(a[1], a[4]); }

if (a[1] > a[2]) { SWAP(a[1], a[2]); }
if (a[3] > a[4]) { SWAP(a[3], a[4]); }
else { goto jump; }

if (a[2] > a[3]) { SWAP(a[2], a[3]); }
jump:;

Я проверил это со всеми перестановками 12345, и он сортирует их все правильно.

Answer 1

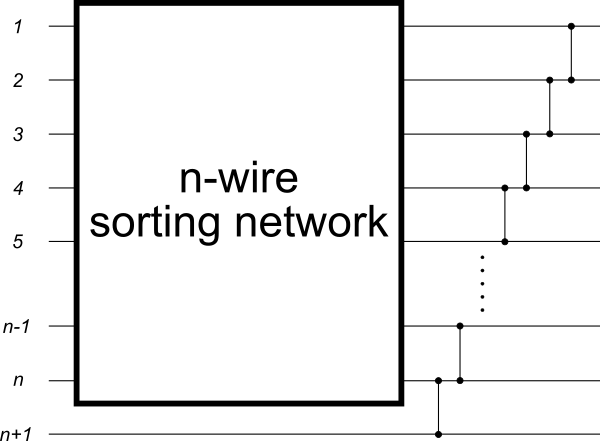
Оставляя в стороне оптимальные сети сортировки, на следующем изображении показан способ создания сети сортировки любого размера n +1 с использованием сети сортировки размера n, а затем выполнения n дополнительных сравнений для размещения последнего элемента на месте (как правило, это сортировка вставкой Работы, переведенные в сортировочную сеть):

Изображение делает это довольно очевидным, чем если бы элемент n +1 уже был самым большим, тогда вы можете пропустить каждый компаратор после того, который сравнивал элементы n и n +1. По существу, когда-нибудь возвращается последний компаратор false Вы пропустите следующие. В общей схеме я бы сказал, что можно было бы пропустить сравнения в большинстве сетей сортировки.

Тем не менее, если у вас есть такие условия в вашем алгоритме сортировки, то это уже не сеть сортировки, и вы теряете преимущества сетей сортировки: при правильной реализации не возникает проблема прогнозирования ветвлений.

Если ваша цель - просто отсортировать небольшую коллекцию, используя как можно меньше сравнений и свопов, вы можете развернуть каждый возможный путь алгоритма сортировки и затем выполнить оптимальное количество ходов / свопов для каждого пути, но такой метод становится прямым выше 4 элементов, и вряд ли у ваших типов есть операции перемещения и сравнения, достаточно дорогие, чтобы оправдать такой алгоритм.