Реализация производной в C/C++
Как производная от f(x) обычно рассчитывается программно для обеспечения максимальной точности?
Я реализую метод Ньютона-Рафсона, и он требует получения производной функции.
8 ответов
Я согласен с @erikkallen, что (f(x + h) - f(x - h)) / 2 * h это обычный подход для численно аппроксимирующих производных. Однако получить правильный размер шага h немного неуловимо.
Ошибка аппроксимации в (f(x + h) - f(x - h)) / 2 * h уменьшается как h становится меньше, что говорит, что вы должны взять h как можно меньше. Но, как h становится меньше, ошибка от вычитания с плавающей запятой увеличивается, поскольку числитель требует вычитать почти равные числа. Если h слишком мал, вы можете потерять много точности в вычитании. Таким образом, на практике вы должны выбрать не слишком маленькое значение h это минимизирует комбинацию ошибки аппроксимации и численной ошибки.
Как правило, вы можете попробовать h = SQRT(DBL_EPSILON) где DBL_EPSILON наименьшее число двойной точности e такой, что 1 + e != 1 в точности машины. DBL_EPSILON около 10^-15 чтобы вы могли использовать h = 10^-7 или же 10^-8,
Для получения дополнительной информации см. Эти примечания по выбору размера шага для дифференциальных уравнений.
Newton_Raphson предполагает, что у вас может быть две функции f(x) и ее производная f'(x). Если у вас нет производной, доступной как функция, и вам необходимо оценить производную от исходной функции, то вам следует использовать другой алгоритм поиска корня.
В корне Википедии можно найти несколько предложений, как и любой текст численного анализа.
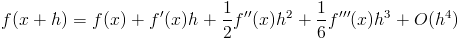
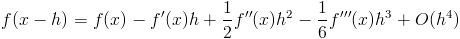
1) Первый случай:
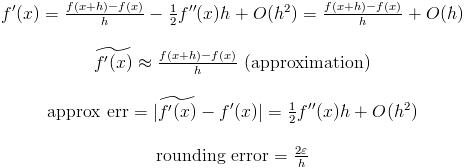
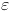- относительная ошибка округления, около 2^{-16} для двойного и 2^{-7} для плавающего.
Мы можем рассчитать общую ошибку:
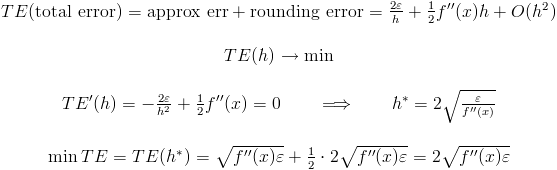
Предположим, что вы используете двойную плавающую операцию. Таким образом, оптимальное значение h равно 2sqrt (DBL_EPSILON /f '' (x)). Вы не знаете f '' (x). Но вы должны оценить это значение. Например, если f '' (x) составляет около 1, то оптимальное значение h равно 2^{-7}, но если f '' (x) составляет около 10^6, то оптимальное значение h равно 2 ^ {- 10}!
2) Второй случай:
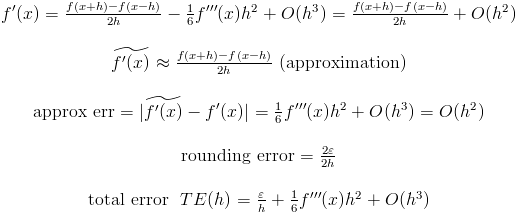
Обратите внимание, что ошибка второго приближения стремится к 0 быстрее, чем первая. Но если f '' '(x) очень запаздывает, тогда первый вариант более предпочтителен:
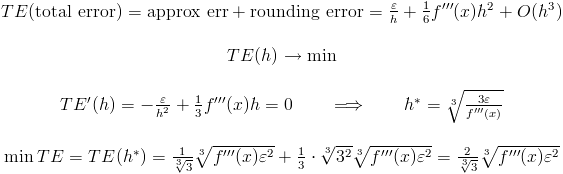
Обратите внимание, что в первом случае h пропорционально e, но во втором случае h пропорционально e^{1/3}. Для операций с плавающей запятой e ^ {1/3} равно 2^{-5} или 2^{-6}. (Я полагаю, что f '' '(x) составляет около 1).
Какой способ лучше? Это неизвестно, если вы не знаете f '' (x) и f '' '(x) или не можете оценить эти значения. Считается, что второй вариант предпочтительнее. Но если вы знаете, что f '' '(x) очень велико, используйте первый.
Какое оптимальное значение h? Предположим, что f '' (x) и f '' '(x) равны 1. Также предположим, что мы используем двойные операции с плавающей запятой. Тогда в первом случае h около 2^{-8}, в первом случае h около 2^{-5}. Исправьте это значение, если вы знаете f '' (x) или f '' '(x).
Что вы знаете о f(x)? Если у вас есть только черный квадрат f, единственное, что вы можете сделать, - это численно аппроксимировать производную. Но точность обычно не так хороша.
Вы можете сделать намного лучше, если вы можете коснуться кода, который вычисляет f. Попробуйте "автоматическое дифференцирование". Есть несколько хороших библиотек для этого. С небольшим количеством волшебства библиотеки вы можете легко преобразовать свою функцию во что-то, что автоматически вычисляет производную. Простой пример C++ см. В исходном коде этого обсуждения на немецком языке.
Вы определенно хотите принять во внимание предложение Джона Кука для выбора h, но обычно вы не хотите использовать центрированную разницу для аппроксимации производной. Основная причина в том, что это требует дополнительной оценки функции, если вы используете прямую разницу, т.е.
f'(x) = (f(x+h) - f(x))/h
Тогда вы получите значение f (x) бесплатно, потому что вам нужно вычислить его уже для метода Ньютона. Это не такая уж большая проблема, когда у вас есть скалярное уравнение, но если x - это вектор, то f '(x) - это матрица (якобиан), и вам нужно будет сделать n дополнительных вычислений функций, чтобы приблизить его используя подход центрированной разницы.
В дополнение к приведенному выше ответу Джона Д. Кука важно учитывать не только точность с плавающей запятой, но и надежность функции f(x). Например, в финансах это частый случай, когда f (x) на самом деле является симуляцией Монте-Карло, и значение f (x) имеет некоторый шум. Использование очень малого размера шага может в этих случаях серьезно ухудшить точность производной.
Обычно шум сигнала влияет на качество производной больше, чем что-либо еще. Если у вас есть шум в вашей f(x), Savtizky-Golay - отличный алгоритм сглаживания, который часто используется для вычисления хороших производных. В двух словах, SG вписывает полином локально в ваши данные, и тогда этот полином можно использовать для вычисления производной.
Павел