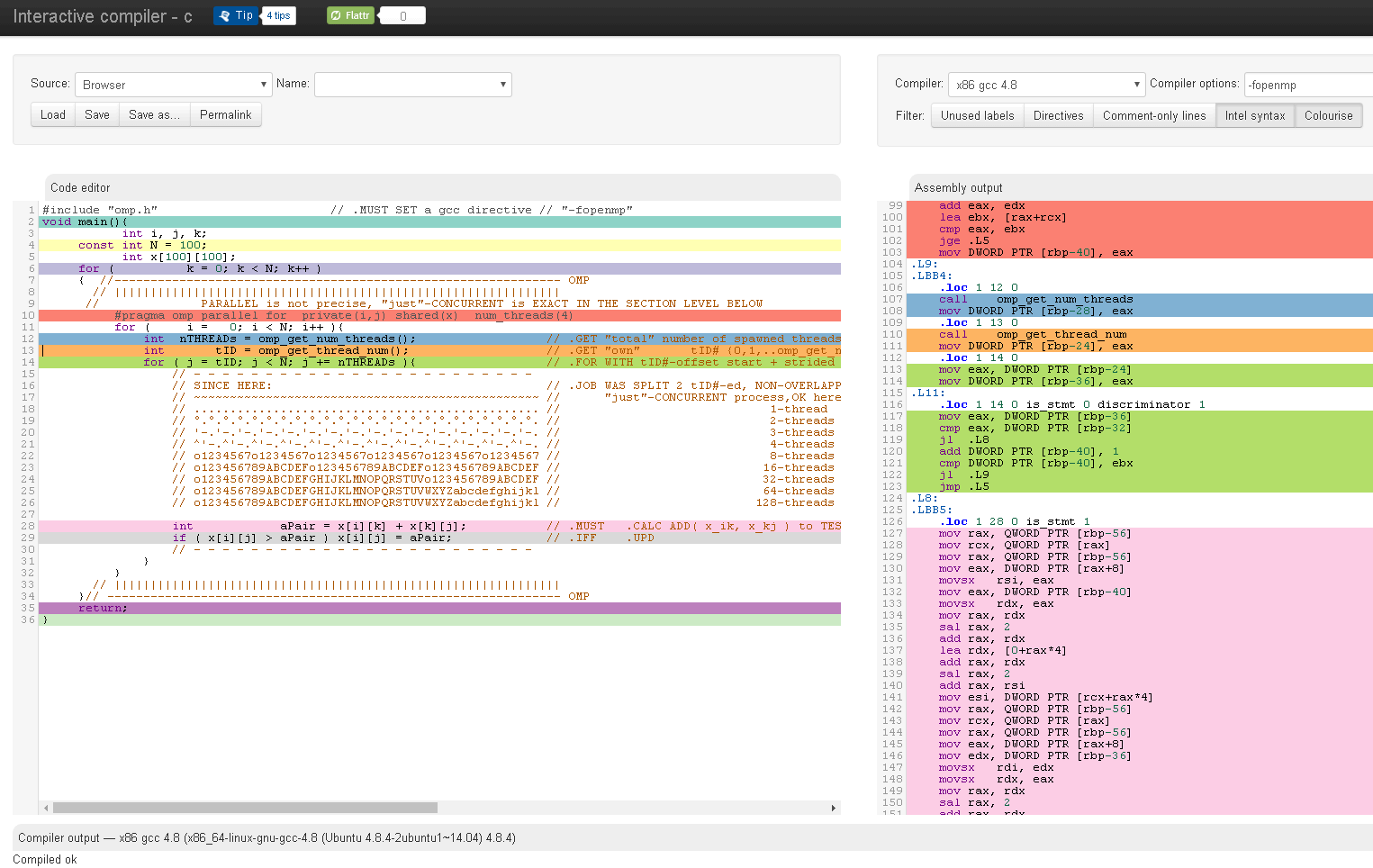
Почему закон Амдаля о последовательных и параллельных дробях не обеспечивает теоретическое ускорение 4 на четырехъядерном процессоре?
У меня есть код
( алгоритм Флойда-Варшалла для кратчайшего пути в NxN матрица),
с тремя for -циклы, один внутри другого и с одинаковым количеством циклов.
Напоследок for У меня есть назначение через троичной операции = <bool> ? <val1> : <val2> - на основе сравнения и если это True или нет.
Я использовал OpenMP для распараллеливания второго for с #pragma ompparallel for,
Я не могу вычислить параллельный процент и последовательный процент кода, чтобы успешно применить закон Амдала для восстановления теоретического ускорения.
for (k = 0; k < N; k++)
#pragma omp parallel for private(i,j) shared(x) num_threads(4)
for (i = 0; i < N; i++){
for (j = 0; j < N; j++) {
x[i][j] = x[i][j] < (x[i][k] + x[k][j]) ? x[i][j] : (x[i][k] + x[k][j]) ;
}
}
Я использую четыре ядра, поэтому я ожидаю теоретическое ускорение 4.
X[i][j] это матрица, где каждый элемент действует как вес ребра, соединяющего узлы i а также j; это макрос INF (бесконечно), если они не связаны.
2 ответа
Два внутренних цикла и тело самого внутреннего цикла выполняются последовательно на каждом ядре. Это потому, что вы пометили внешний цикл для параллельного выполнения.
Но:
- Я ожидал бы намного меньше, чем ускорение 4. Всегда есть коммуникационные издержки
Тело в самом внутреннем цикле использует одну и ту же матрицу для всех ядер, а также модифицирует матрицу. поэтому изменения в матрице должны распространяться на все остальные ядра. Это может привести к следующим проблемам:
- Кеши ЦП могут быть бесполезны, поскольку элементы кэшированного массива могут быть изменены другим ядром, которое может иметь другой кеш.
- В худшем случае все модификации в матрице зависят от предыдущего изменения (я не проверял это для вашего случая). В этом случае параллельное выполнение невозможно => вообще никакого ускорения для более чем одного ядра.
Вы должны проверить, возможно ли изменить ваш алгоритм таким образом, чтобы не пересекались частичные матрицы. Вы получите лучшее ускорение, если ядра будут работать с отдельными непересекающимися данными.
Поскольку при этом почти нет усилий, вам следует определенно профилировать код и его варианты.
TL;DR:
замечательно, что университеты проводят больше времени на практических примерах Закона Амдала, чтобы показать, как легко девочки и мальчики, занимающиеся маркетингом, создают ложные ожидания в отношении многоядерных и многоядерных игрушек.
Тем не менее, давайте определим тест-кейс:
Проблема в Floyd-Warshall Processing может быть структурирована в:
- издержки запуска процесса
- распределение памяти по структурам данных + настройка
- инициализация значений данных
- Особые условия Флойда-Варшалла (нулевая диагональ и т. Д.)
- Инструменты хронометража
- Секция с процессом Флойда-Варшалла O(N^3) с потенциальным улучшением в процессе тестирования [IUT]
Закон Амдала объявляет предельный предел для любого общего "улучшения" Процесса, учитывая, что в разделе [6] содержится [IUT] для оценки, в то время как общее "улучшение" НИКОГДА не станет лучше, чем ~ 1 / ( ( 1 - IUT ) + ( IUT / N ) ),
Добрые читатели должны проверить и записать время для ( 1 - IUT ) часть эксперимента.
Как вычислить эффект потенциально распараллеленного [IUT] в разделе [6] кода?
Во-первых, давайте сосредоточимся на том, что происходит в первоначально опубликованном коде, в чистом виде. SEQ (последовательный) поток выполнения кода:
В исходном фрагменте уже было место для улучшения производительности, даже без попытки на основе OpenMP распределить задачу по большей базе ресурсов:
for ( k = 0; k < N; k++ )
for ( i = 0; i < N; i++ ){
for ( j = 0; j < N; j++ ){
x[i][j] = x[i][j] > ( x[i][k] + x[k][j] ) // .TEST <bool>
? ( x[i][k] + x[k][j] ) // .ASSIGN <val1>
: x[i][j]; // .ASSIGN <val2>
}
}
Если бы это было запущено как чисто SEQ соло или при попытке использовать #pragma omp Как было написано в первоначальном вопросе, в обоих случаях закон Амдала покажет НОЛЬ или даже "отрицательное" улучшение.
Зачем? Почему бы не ускорить 4? Почему вообще нет улучшений?
Так как код был проинструктирован для выполнения "механически", повторяющегося на всех ресурсах, при одинаковом выполнении одинаковой области действия задачи для полных 4 раз, плечом к плечу, причем каждый из них, кроме других, то в 4 раза больше ресурсов не принести ожидаемого положительного эффекта, так как они вместе потратили одно и то же время на 4-хкратное выполнение всех частей задачи независимо друг от друга на потенциальной "помощи" других (если не хуже, в некоторых случаях, когда нехватка ресурсов наблюдалась в течение всего выполнения задачи).
Итак, давайте лучше воспользуемся преимуществами OpenMP, чтобы разделить задачу, и пусть каждый ресурс обрабатывает только адекватную часть объема алгоритма (благодаря алгоритму Флойда-Варшалла, поскольку это очень простое в этом направлении и позволяет поскольку его схема обработки, даже когда разрешены отрицательные веса, не является вмешательством, поэтому для распространения чего-либо среди потоков не требуется никаких враждебных барьеров, синхронизаций, критического сечения)
Итак, можем ли мы получить какие-либо преимущества OpenMP здесь? Ах да, много
#include "omp.h" // .MUST SET a gcc directive // "-fopenmp"
// --------------------------------------------------------[1] ref. above
void main(){
int i, j, k;
const int N = 100;
int x[100][100];
// --------------------------------------------------------[2] ref. above
// --------------------------------------------------------[3] ref. above
// --------------------------------------------------------[4] ref. above
for ( k = 0; k < N; k++ )
{
// --------------------------------------------------------[5] ref. above
//------------------------------------------------------[6]----- OMP
// ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
// PARALLEL is not precise, "just"-CONCURRENT is EXACT IN THE SECTION LEVEL BELOW
#pragma omp parallel for private(i,j) shared(x) num_threads(4)
for ( i = 0; i < N; i++ ){ // .MUST incl.actual k-th ROW, in case NEG weights are permitted
int nTHREADs = omp_get_num_threads(); // .GET "total" number of spawned threads
int tID = omp_get_thread_num(); // .GET "own" tID# {0,1,..omp_get_num_threads()-1} .AVOID dumb repeating the same .JOB by all spawned threads
for ( j = tID; j < N; j += nTHREADs ){ // .FOR WITH tID#-offset start + strided .INC STEP // .MUST incl.actual k-th COL, in case NEG weights are permitted
// - - - - - - - - - - - - - - - - - - - - - - - -
// SINCE HERE: // .JOB WAS SPLIT 2 tID#-ed, NON-OVERLAPPING tasks
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // .N.B: dumb "just"-CONCURRENT processing is O.K. here
// ................................................ // 1-thread .INC STEP +1 a sure ZERO Amdahl-Law effect ( will bear an adverse penalty from use-less omp_get_*() calls )
// °.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°.°. // 2-threads .INC STEP +2 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 2 ) ) if enough free CPU-resources
// '-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-.'-. // 3-threads .INC STEP +3 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 3 ) ) if enough free CPU-resources
// ^'-.^'-.^'-.^'-.^'-.^'-.^'-.^'-.^'-.^'-.^'-.^'-. // 4-threads .INC STEP +4 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 4 ) ) if enough free CPU-resources
// o1234567o1234567o1234567o1234567o1234567o1234567 // 8-threads .INC STEP +8 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 8 ) ) if enough free CPU-resources
// o123456789ABCDEFo123456789ABCDEFo123456789ABCDEF // 16-threads .INC STEP +16 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 16 ) ) if enough free CPU-resources
// o123456789ABCDEFGHIJKLMNOPQRSTUVo123456789ABCDEF // 32-threads .INC STEP +32 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 32 ) ) if enough free CPU-resources
// o123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijkl // 64-threads .INC STEP +64 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 64 ) ) if enough free CPU-resources
// o123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijkl // 128-threads .INC STEP +128 may have Amdahl-Law effect ~ 1 / ( ( 1 - OMP ) + ( OMP / 128 ) ) if enough free CPU-resources
int aPair = x[i][k] + x[k][j]; // .MUST .CALC ADD( x_ik, x_kj ) to TEST // .MAY smart re-use in case .GT. and ASSIGN will have to take a due place
if ( x[i][j] > aPair ) x[i][j] = aPair; // .IFF .UPD // .AVOID dumb re-ASSIGN(s) of self.value(s) to self
// - - - - - - - - - - - - - - - - - - - - - - - -
}
}
// ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
}// --------------------------------------------------------------- OMP
return;
}
Понимание OpenMP за пределами предсказанного предела закона Амдала:
Предлагаемый подход открывает некоторый потенциал для дальнейшего исследования с помощью забавных экспериментов:
- установить количество потоков как 1 (для использования в качестве основы эксперимента)
- установить количество потоков как ( nCPUcores / 2)
- установить количество потоков как ( nCPUcores - 1)
- установить количество потоков как ( nCPUcores) + запустить дефрагментацию / сжатие диска
- установить количество потоков как ( nCPUcores * 2)
- установить количество потоков как ( nCPUcores * 2) + обеспечить привязку к процессору только на 2 процессорных ядрах
- установить количество потоков как ( nCPUcores * 20)
- установить количество строк / столбцов N ~ { 1.000 | 10.000 | 100.000 | 1.000.000 } и проверьте эффекты