Что такое функтор в функциональном программировании?

Я встречал термин "Functor" несколько раз, читая различные статьи о функциональном программировании, но авторы обычно предполагают, что читатель уже понимает этот термин. Просмотр в Интернете предоставил либо чрезмерно технические описания (см. Статью в Википедии), либо невероятно расплывчатые описания (см. Раздел "Функторы" на этом веб-сайте ocaml-учебника).

Может ли кто-нибудь любезно дать определение термину, объяснить его использование и, возможно, привести пример того, как создаются и используются функторы?

Изменить: Хотя меня интересует теория, стоящая за этим термином, меня интересует не столько теория, сколько реализация и практическое использование концепции.

Редактировать 2: Похоже, что происходит некоторая кросс-терминология: я специально имею в виду Функторы функционального программирования, а не функциональные объекты C++.

Источник

19 ответов

Решение

Слово "функтор" происходит от теории категорий, которая является очень общей, очень абстрактной областью математики. Он был заимствован дизайнерами функциональных языков как минимум двумя различными способами.

  • В семействе языков ML функтор - это модуль, который принимает один или несколько других модулей в качестве параметра. Это считается расширенной функцией, и большинство начинающих программистов испытывают трудности с этим.

    В качестве примера реализации и практического использования вы можете раз и навсегда определить вашу любимую форму сбалансированного бинарного дерева поиска как функтор, и в качестве параметра он будет принимать модуль, который обеспечивает:

    • Тип ключа, который будет использоваться в двоичном дереве

    • Функция полного заказа на клавиши

    Как только вы это сделаете, вы можете использовать одну и ту же сбалансированную двоичную реализацию дерева навсегда. (Тип значения, хранящегося в дереве, обычно остается полиморфным - дереву не нужно смотреть на значения, кроме как копировать их, тогда как дерево определенно должно иметь возможность сравнивать ключи, и оно получает функцию сравнения из параметр функтора.)

    Другое применение функторов ML - многоуровневые сетевые протоколы. Ссылка на действительно потрясающую статью группы CMU Fox; в нем показано, как использовать функторы для построения более сложных протокольных уровней (например, TCP) на типах более простых уровней (например, IP или даже напрямую через Ethernet). Каждый слой реализован как функтор, который принимает в качестве параметра слой под ним. Структура программного обеспечения фактически отражает то, как люди думают о проблеме, в отличие от уровней, существующих только в сознании программиста. В 1994 году, когда эта работа была опубликована, это было большое дело.

    Для дикого примера ML-функторов в действии вы можете увидеть статью ML Module Mania, которая содержит публикуемый (то есть, страшный) пример функторов в действии. Чтобы получить блестящее, ясное и ясное объяснение системы модулей ML (со сравнениями с другими типами модулей), прочитайте первые несколько страниц блестящей POPL-публикации Ксавьера Лероя 1994 года " Типы манифестов, модули и отдельная компиляция".

  • В Haskell и в некотором родственном чисто функциональном языке Functor это класс типа. Тип принадлежит классу типа (или, более технически, тип "является экземпляром" класса типа), когда тип обеспечивает определенные операции с определенным ожидаемым поведением. Тип T может принадлежать к классу Functor если он имеет определенное поведение, похожее на коллекцию:

    • Тип T параметризован по другому типу, который вы должны рассматривать как тип элемента коллекции. Тип полной коллекции - это что-то вроде T Int, T String, T Bool, если вы содержите целые числа, строки или логические значения соответственно. Если тип элемента неизвестен, он записывается как параметр типа a, как в T a,

      Примеры включают списки (ноль или более элементов типа a), Maybe тип (ноль или один элемент типа a), наборы элементов типа a, массивы элементов типа a, все виды деревьев поиска, содержащие значения типа a и много других, о которых вы можете подумать.

    • Другое свойство, которое T должен удовлетворить, что если у вас есть функция типа a -> b (функция для элементов), тогда вы должны иметь возможность взять эту функцию и создать связанную функцию для коллекций. Вы делаете это с оператором fmap, который является общим для каждого типа в Functor тип класс. Оператор действительно перегружен, так что если у вас есть функция even с типом Int -> Bool, затем

      fmap even

      перегруженная функция, которая может делать много замечательных вещей:

      • Преобразовать список целых чисел в список логических значений

      • Преобразовать дерево целых чисел в дерево логических

      • Перерабатывать Nothing в Nothing а также Just 7 в Just False

      В Хаскеле это свойство выражается путем указания типа fmap:

      fmap :: (Functor t) => (a -> b) -> t a -> t b

      где у нас сейчас есть маленький t, что означает "любой тип в Functor учебный класс."

    Короче говоря, в Haskell функтор - это своего рода коллекция, для которой, если вам дают функцию над элементами, fmap вернет вам функцию по коллекциям. Как вы можете себе представить, это идея, которую можно широко использовать, поэтому она является частью стандартной библиотеки Haskell.

Как обычно, люди продолжают изобретать новые, полезные абстракции, и вы можете захотеть взглянуть на аппликативные функторы, для которых лучшим справочным материалом может стать статья " Аппликативное программирование с эффектами " Конора МакБрайда и Росса Патерсона.

Источник

Другие ответы здесь полны, но я попробую другое объяснение использования функтора в FP. Возьмем это как аналогию:

Функтор - это контейнер типа a, который при воздействии на функцию, отображающую из a→b, дает контейнер типа b.

В отличие от использования указателя на абстрагированную функцию в C++, здесь функтор не является функцией; скорее это то, что ведет себя последовательно, когда подвергается функции.

Источник

Есть три разных значения, мало связанных между собой!

  • В Ocaml это параметризованный модуль. Смотрите руководство. Я думаю, что лучший способ получить их - это пример: (написано быстро, может быть глючит)

    module type Order = sig
    type t
    val compare: t -> t -> bool
end;;


module Integers = struct
    type t = int
    let compare x y = x > y
end;;

module ReverseOrder = functor (X: Order) -> struct
    type t = X.t
    let compare x y = X.compare y x
end;;

(* We can order reversely *)
module K = ReverseOrder (Integers);;
Integers.compare 3 4;;   (* this is false *)
K.compare 3 4;;          (* this is true *)

module LexicographicOrder = functor (X: Order) -> 
  functor (Y: Order) -> struct
    type t = X.t * Y.t
    let compare (a,b) (c,d) = if X.compare a c then true
                         else if X.compare c a then false
                         else Y.compare b d
end;;

(* compare lexicographically *)
module X = LexicographicOrder (Integers) (Integers);;
X.compare (2,3) (4,5);;

module LinearSearch = functor (X: Order) -> struct
    type t = X.t array
    let find x k = 0 (* some boring code *)
end;;

module BinarySearch = functor (X: Order) -> struct
    type t = X.t array
    let find x k = 0 (* some boring code *)
end;;

(* linear search over arrays of integers *)
module LS = LinearSearch (Integers);;
LS.find [|1;2;3] 2;;
(* binary search over arrays of pairs of integers, 
   sorted lexicographically *)
module BS = BinarySearch (LexicographicOrder (Integers) (Integers));;
BS.find [|(2,3);(4,5)|] (2,3);;

Теперь вы можете быстро добавлять множество возможных заказов, способы формирования новых заказов, легко выполнять бинарный или линейный поиск по ним. Универсальное программирование FTW.

  • В функциональных языках программирования, таких как Haskell, это означает некоторые конструкторы типов (параметризованные типы, такие как списки, множества), которые могут быть отображены. Чтобы быть точным, функтор f оснащен (a -> b) -> (f a -> f b), Это имеет начало в теории категорий. Статья Википедии, на которую вы ссылаетесь, является этим использованием.

    class Functor f where
    fmap :: (a -> b) -> (f a -> f b)

instance Functor [] where      -- lists are a functor
    fmap = map

instance Functor Maybe where   -- Maybe is option in Haskell
    fmap f (Just x) = Just (f x)
    fmap f Nothing = Nothing

fmap (+1) [2,3,4]   -- this is [3,4,5]
fmap (+1) (Just 5)  -- this is Just 6
fmap (+1) Nothing   -- this is Nothing

Итак, это особый тип конструкторов типов, и он не имеет ничего общего с функторами в Ocaml!

  • В императивных языках это указатель на функцию.
Источник

Вы получили довольно много хороших ответов. Я передам:

Функтор в математическом смысле представляет собой особый вид функции в алгебре. Это минимальная функция, которая отображает алгебру в другую алгебру. "Минимальность" выражается законами функтора.

Есть два способа посмотреть на это. Например, списки являются функторами некоторого типа. То есть, учитывая алгебру над типом "а", вы можете сгенерировать совместимую алгебру списков, содержащих вещи типа "а". (Например: карта, которая переводит элемент в одноэлементный список, содержащий его: f(a) = [a]) Опять же, понятие совместимости выражается законами функторов.

С другой стороны, учитывая, что функтор f "над" типом a (то есть fa является результатом применения функтора f к алгебре типа a) и функции из g: a -> b, мы можем вычислить новый функтор F = (fmap g), который отображает fa на f b. Короче говоря, fmap - это часть F, которая отображает "части функтора" на "части функтора", а g - это часть функции, которая отображает "части алгебры" в "части алгебры". Он принимает функцию, функтор, и когда он завершен, он тоже является функтором.

Может показаться, что разные языки используют разные понятия функторов, но это не так. Они просто используют функторы над различными алгебрами. У OCamls есть алгебра модулей, а функторы над этой алгеброй позволяют вам присоединять новые объявления к модулю "совместимым" способом.

Функтор Haskell НЕ является классом типа. Это тип данных со свободной переменной, который удовлетворяет классу типа. Если вы хотите разобраться в типах данных (без свободных переменных), вы можете переосмыслить тип данных как функтор над базовой алгеброй. Например:

данные F = F Int

изоморфен классу инт. Таким образом, F, как конструктор значений, является функцией, которая отображает Int в F Int, эквивалентную алгебру. Это функтор. С другой стороны, вы не получаете fmap бесплатно здесь. Вот для чего нужно сопоставление с образцом.

Функторы хороши для "прикрепления" вещей к элементам алгебры алгебраически совместимым способом.

Источник

В OCaml это параметризованный модуль.

Если вы знаете C++, подумайте о функторе OCaml как о шаблоне. В C++ есть только шаблоны классов, а функторы работают в масштабе модуля.

Примером функтора является Map.Make; module StringMap = Map.Make (String);; создает модуль карты, который работает с картами со строковыми ключами.

Вы не могли бы достичь чего-то вроде StringMap только с полиморфизмом; вам нужно сделать некоторые предположения о ключах. Модуль String содержит операции (сравнение и т. Д.) Для полностью упорядоченного строкового типа, а функтор будет связывать операции, содержащиеся в модуле String. Вы можете сделать что-то подобное с объектно-ориентированным программированием, но у вас будут накладные расходы на метод.

Источник

Лучший ответ на этот вопрос найден в "Typeclassopedia" Brent Yorgey.

В этом выпуске Monad Reader содержится точное определение того, что такое функтор, а также множество определений других понятий и диаграммы. (Monoid, Applicative, Monad и другие концепции объясняются и рассматриваются по отношению к функтору).

http://haskell.org/sitewiki/images/8/85/TMR-Issue13.pdf

выдержка из Typeclassopedia для Functor: "Простая интуиция заключается в том, что Functor представляет некоторый" контейнер "вместе с возможностью равномерно применять функцию к каждому элементу в контейнере"

Но на самом деле вся тип-классопедия очень рекомендуется для чтения, что удивительно легко. В некотором смысле вы можете видеть представленный там класс типов как параллель к шаблону проектирования в объекте в том смысле, что они дают вам словарный запас для данного поведения или возможностей.

ура

Источник

Есть довольно хороший пример в книге O'Reilly OCaml, которая находится на веб-сайте Инрии (которая на момент написания статьи, к сожалению, не работает). В этой книге я нашел очень похожий пример, используемый caltech: Введение в OCaml (pdf link). Соответствующим разделом является глава о функторах (стр. 139 в книге, стр. 149 в PDF).

В книге есть функтор MakeSet, который создает структуру данных, состоящую из списка, и функции для добавления элемента, определения наличия элемента в списке и поиска элемента. Функция сравнения, которая используется для определения того, находится ли она в / не в наборе, была параметризована (что делает MakeSet функтором вместо модуля).

У них также есть модуль, который реализует функцию сравнения, так что он выполняет сравнение строк без учета регистра.

Используя функтор и модуль, который реализует сравнение, они могут создать новый модуль в одну строку:

module SSet = MakeSet(StringCaseEqual);;

это создает модуль для заданной структуры данных, которая использует сравнения без учета регистра. Если вы хотите создать набор, в котором используются сравнения с учетом регистра, вам просто нужно реализовать новый модуль сравнения вместо нового модуля структуры данных.

Тобу сравнил функторы с шаблонами в C++, которые я считаю вполне подходящими.

Источник

"Функтор - это отображение объектов и морфизмов, которое сохраняет композицию и идентичность категории".

Давайте определим, что такое категория?

Это куча предметов!

Нарисуйте несколько точек (на данный момент 2 точки, одна - "a", другая - "b") внутри круга и назовите этот круг A(Категория).

Что держит категория?

Композиция между объектами и функция идентичности для каждого объекта.

Итак, мы должны отобразить объекты и сохранить композицию после применения нашего Functor.

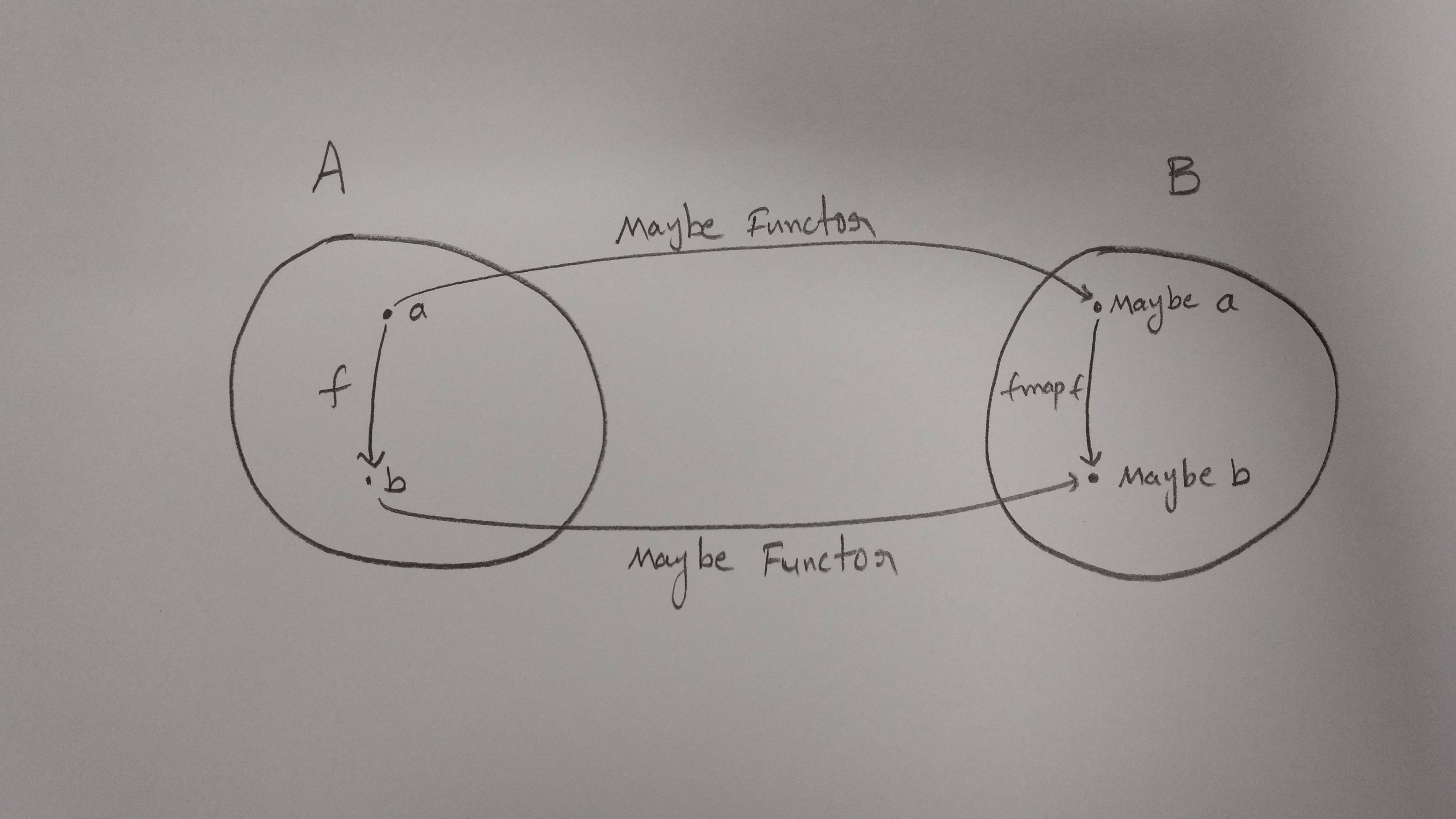
Давайте представим, что "A" - это наша категория, в которой есть объекты ['a', 'b'] и существует морфизм a -> b

Теперь нам нужно определить функтор, который может отобразить эти объекты и морфизмы в другую категорию "B".

Допустим, функтор называется "Может быть"

data Maybe a = Nothing | Just a

Итак, категория "В" выглядит следующим образом.

Пожалуйста, нарисуйте еще один круг, но на этот раз с "Возможно a" и "Возможно b" вместо "a" и "b".

Все выглядит хорошо, и все объекты сопоставлены

"а" стало "может быть", а "б" стало "возможно, б".

Но проблема в том, что мы также должны сопоставить морфизм от "а" до "б".

Это означает, что морфизм a -> b в "A" должен соответствовать морфизму "Maybe a" -> "Maybe b".

морфизм из a -> b называется f, затем морфизм из 'Maybe a' -> 'Maybe b' называется 'fmap f'

Теперь давайте посмотрим, что функция "f" делала в "A", и посмотрим, сможем ли мы повторить ее в "B".

определение функции 'f' в 'A':

f :: a -> b

е берет а возвращает б

определение функции 'f' в 'B':

f :: Maybe a -> Maybe b

f берет Может а и возвращает Может б

давайте посмотрим, как использовать fmap для отображения функции 'f' из 'A' в функцию 'fmap f' в 'B'

определение fmap

fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap f Nothing = Nothing
fmap f (Just x) = Just(f x)

Итак, что мы здесь делаем?

Мы применяем функцию "f" к "x", которая имеет тип "a". Специальное сопоставление с образцом "Ничего" происходит из определения Functor Maybe,

Итак, мы отобразили наши объекты [a, b] и морфизмы [f] из категории "A" в категорию "B".

Это Функтор!

Источник

Учитывая другие ответы и то, что я собираюсь опубликовать сейчас, я бы сказал, что это довольно сильно перегруженное слово, но в любом случае...

Чтобы получить подсказку о значении слова "функтор" в Haskell, спросите GHCi:

Prelude> :info Functor
class Functor f where
  fmap :: forall a b. (a -> b) -> f a -> f b
  (GHC.Base.<$) :: forall a b. a -> f b -> f a
        -- Defined in GHC.Base
instance Functor Maybe -- Defined in Data.Maybe
instance Functor [] -- Defined in GHC.Base
instance Functor IO -- Defined in GHC.Base

Так что, по сути, функтор в Haskell - это то, что можно сопоставить. Другой способ сказать, что функтор - это нечто, что можно рассматривать как контейнер, который можно попросить использовать данную функцию для преобразования значения, которое он содержит; таким образом, для списков, fmap совпадает с map, за Maybe, fmap f (Just x) = Just (f x), fmap f Nothing = Nothing и т.п.

В подразделе классов типов Functor и в разделе " Функторы, аппликативные функторы и моноиды " вы учите хакелл для великого добра "" приведены некоторые примеры того, как эта конкретная концепция полезна. (Резюме: много мест!:-))

Обратите внимание, что любую монаду можно рассматривать как функтор, и на самом деле, как указывает Крейг Штунц, наиболее часто используемые функторы, как правило, являются монадами... ОТО, иногда удобно сделать тип экземпляром класса типов Functor не вдаваясь в проблемы сделать его монадой. (Например, в случае ZipList от Control.Applicative упоминается на одной из вышеупомянутых страниц.)

Источник

В комментарии к ответу, получившему Wei Hu голосов, пользователь Wei Hu спрашивает:

Я понимаю и ML-функторы, и Haskell-функторы, но мне не хватает понимания, чтобы связать их вместе. Какая связь между этими двумя в теоретико-категориальном смысле?

Примечание: я не знаю ML, поэтому, пожалуйста, простите и исправьте все ошибки.

Давайте сначала предположим, что мы все знакомы с определениями "категория" и "функтор".

Компактным ответом будет то, что "функторы Хаскеля" являются (эндо-) функторами F : Hask -> Hask в то время как "ML-функторы" являются функторами G : ML -> ML',

Вот, Hask категория, образованная типами и функциями Haskell между ними, и аналогично ML а также ML' категории, определенные структурами ML.

Примечание: есть некоторые технические проблемы с Hask категория, но есть способы обойти их.

С теоретической точки зрения категории это означает, что Hask -функтор это карта F типов Haskell:

data F a = ...

вместе с картой fmap функций Haskell:

instance Functor F where
    fmap f = ...

ML почти такой же, хотя нет канонического fmap абстракция мне известна, поэтому давайте определим одну:

signature FUNCTOR = sig
  type 'a f
  val fmap: 'a -> 'b -> 'a f -> 'b f
end

То есть f карты ML -типы и fmap карты ML -функции, так

functor StructB (StructA : SigA) :> FUNCTOR =
struct
  fmap g = ...
  ...
end

это функтор F: StructA -> StructB,

Источник

Вот статья о функторах из POV программирования, а затем более конкретно о том, как они появляются в языках программирования.

Практическое использование функтора в монаде, и вы можете найти много уроков по монадам, если посмотрите на это.

Источник

Грубый Обзор

В функциональном программировании функтор - это, по сути, конструкция, поднимающая обычные унарные функции (т. Е. С одним аргументом) в функции между переменными новых типов. Гораздо проще писать и поддерживать простые функции между простыми объектами и использовать функторы для их подъема, а затем вручную писать функции между сложными объектами-контейнерами. Еще одним преимуществом является написание простых функций только один раз, а затем их повторное использование через различные функторы.

Примеры функторов включают массивы, функторы "возможно" и "либо", фьючерсы (см., Например, https://github.com/Avaq/Fluture) и многие другие.

иллюстрация

Рассмотрим функцию построения полного имени человека из имени и фамилии. Мы могли бы определить это как fullName(firstName, lastName) как функция двух аргументов, что, однако, не подходит для функторов, которые имеют дело только с функциями одного аргумента. Для исправления мы собираем все аргументы в один объект name, который теперь становится единственным аргументом функции:

// In JavaScript notation
fullName = name => name.firstName + ' ' + name.lastName

А что если у нас много людей в массиве? Вместо того, чтобы вручную просматривать список, мы можем просто повторно использовать нашу функцию fullName через map метод, предусмотренный для массивов с короткой строкой кода:

fullNameList = nameList => nameList.map(fullName)

и использовать его как

nameList = [
    {firstName: 'Steve', lastName: 'Jobs'},
    {firstName: 'Bill', lastName: 'Gates'}
]

fullNames = fullNameList(nameList) 
// => ['Steve Jobs', 'Bill Gates']

Это будет работать, когда каждая запись в нашем nameList является объектом, обеспечивающим как firstName а также lastName свойства. Но что если некоторые объекты этого не делают (или вообще не являются объектами)? Чтобы избежать ошибок и сделать код более безопасным, мы можем обернуть наши объекты в Maybe тип (например, https://sanctuary.js.org/):

// function to test name for validity
isValidName = name => 
    (typeof name === 'object') 
    && (typeof name.firstName === 'string')
    && (typeof name.lastName === 'string')

// wrap into the Maybe type
maybeName = name => 
    isValidName(name) ? Just(name) : Nothing()

где Just(name) это контейнер, содержащий только действительные имена и Nothing() это специальное значение, используемое для всего остального. Теперь вместо того, чтобы прерывать (или забывать) проверять правильность наших аргументов, мы можем просто повторно использовать (поднять) наш оригинал fullName функция с другой строкой кода, снова на основе map метод, на этот раз предусмотрен для типа Maybe:

// Maybe Object -> Maybe String
maybeFullName = maybeName => maybeName.map(fullName)

и использовать его как

justSteve = maybeName(
    {firstName: 'Steve', lastName: 'Jobs'}
) // => Just({firstName: 'Steve', lastName: 'Jobs'})

notSteve = maybeName(
    {lastName: 'SomeJobs'}
) // => Nothing()

steveFN = maybeFullName(justSteve)
// => Just('Steve Jobs')

notSteveFN = maybeFullName(notSteve)
// => Nothing()

Теория категорий

Функтор в теории категорий - это карта между двумя категориями, соблюдающая композицию их морфизмов. В компьютерном языке основной интересующей категорией является та, чьи объекты являются типами (определенными наборами значений), а чьи морфизмы являются функциями f:a->b от одного типа a к другому типу b,

Например, взять a быть String тип, b Тип номера и f является функцией, отображающей строку в ее длину:

// f :: String -> Number
f = str => str.length

Вот a = String представляет собой набор всех строк и b = Number множество всех чисел. В этом смысле оба a а также b представляют объекты в категории "Set" (которая тесно связана с категорией типов, с разницей здесь несущественной). В категории множеств морфизмы между двумя наборами являются точно всеми функциями из первого множества во второе. Так что наша функция длины f вот морфизм из набора строк в набор чисел.

Поскольку мы рассматриваем только заданную категорию, соответствующие Функторы из нее в себя являются картами, отправляющими объекты объектам, и морфизмы в морфизмы, которые удовлетворяют определенным алгебраическим законам.

Пример: Array

Array может означать много вещей, но только одна вещь - это Functor - конструкция типа, отображающая тип a в тип [a] всех массивов типа a, Например, Array функтор отображает тип String в тип [String] (множество всех массивов строк произвольной длины) и тип набора Number в соответствующий тип [Number] (множество всех массивов чисел).

Важно не путать карту Функтора

Array :: a => [a]

с морфизмом a -> [a], Функтор просто отображает (ассоциирует) тип a в тип [a] как одно в другое. То, что каждый тип на самом деле представляет собой набор элементов, здесь не имеет значения. Напротив, морфизм является действительной функцией между этими наборами. Например, существует естественный морфизм (функция)

pure :: a -> [a]
pure = x => [x]

который отправляет значение в массив из 1 элемента с этим значением в виде одной записи. Эта функция не является частью Array Функтор! С точки зрения этого функтора, pure это просто функция, как и любая другая, ничего особенного.

С другой стороны, Array Функтор имеет вторую часть - часть морфизма. Какие карты морфизма f :: a -> b в морфизм [f] :: [a] -> [b]:

// a -> [a]
Array.map(f) = arr => arr.map(f)

Вот arr любой массив произвольной длины со значениями типа a, а также arr.map(f) массив одинаковой длины со значениями типа bчьи записи являются результатами применения f на записи arr, Чтобы сделать его функтором, должны соблюдаться математические законы отображения идентичности на идентичность и композиций на композиции, что легко проверить в этом Array пример.

Источник

KISS: функтор - это объект, у которого есть метод карты.

Массивы в JavaScript реализуют карту и поэтому являются функторами. Обещания, потоки и деревья часто реализуют карту на функциональных языках, и когда они это делают, они считаются функторами. Метод map функтора берет свое собственное содержимое и преобразует каждое из них, используя обратный вызов преобразования, переданный в map, и возвращает новый функтор, который содержит структуру в качестве первого функтора, но с преобразованными значениями.

источник: https://www.youtube.com/watch?v=DisD9ftUyCk&feature=youtu.be&t=76

Источник

Не противоречит предыдущим теоретическим или математическим ответам, но Функтор также является Объектом (на объектно-ориентированном языке программирования), который имеет только один метод и эффективно используется в качестве функции.

Примером является интерфейс Runnable в Java, который имеет только один метод: run.

Рассмотрим этот пример, сначала в Javascript, который имеет функции первого класса:

[1, 2, 5, 10].map(function(x) { return x*x; });

Выход: [1, 4, 25, 100]

Метод map принимает функцию и возвращает новый массив, каждый элемент которого является результатом применения этой функции к значению в той же позиции в исходном массиве.

Чтобы сделать то же самое с Java, используя Functor, вам сначала нужно определить интерфейс, скажем:

public interface IntMapFunction {
  public int f(int x);
}

Затем, если вы добавите класс коллекции, у которого есть функция карты, вы можете сделать:

myCollection.map(new IntMapFunction() { public int f(int x) { return x * x; } });

При этом используется встроенный подкласс IntMapFunction для создания Functor, который является ОО-эквивалентом функции из более раннего примера JavaScript.

Использование Функторов позволяет применять функциональные методы на языке ОО. Конечно, некоторые языки OO также поддерживают функции напрямую, так что это не обязательно.

Ссылка: http://en.wikipedia.org/wiki/Function_object

Источник

Функтор — это объект класса, который ведет себя как функция.

      inky_the_inkrementor = Inkrementor(1)
# running total is 1

inky_the_inkrementor(10)
# running total is 11

inky_the_inkrementor(100) 
# running total is 111

inky_the_inkrementor(1000)
# running total is 1111

inky_the_inkrementor(10000) 
# running total is 11111

inky_the_inkrementor(100000)
# running total is 111111

inky_the_inkrementor(9)(1)(10)(100)
# running total is 111111

inky_the_inkrementor(500000, 50000, 5000)
# the running total is 1555111

print(int(inky_the_inkrementor))
# prints 1555111

После того, как вы создадите экземпляр функтора , вы сможете написать()на правой стороне.

Ниже у нас есть примеры функтора, написанного на Python.

Питон

      class Inkrementor:

    def __init__(this, *args):
        this._num = 0
        this(*args)

    def __call__(this, *args):
        left      = float(args[0])

        leftovers = this(*args[1:])

        this._num += left + leftovers

        return this 

    def __float__(this):
        return this._num
Источник

В функциональном программировании обработка ошибок отличается. Генерация и перехват исключений — это императивный код. Вместо использования блок, вокруг кода создается защитная рамка, которая может вызвать ошибку. это фундаментальный шаблон проектирования в функциональном программировании. Объект-оболочка используется для инкапсуляции потенциально ошибочного значения. Основная цель оболочки - предоставить «другой» способ использования обернутого объекта.

       const wrap = (val) => new Wrapper(val);

Обертка обеспечивает прямой доступ к значениям, чтобы ими можно было безопасно и неизменно манипулировать. Поскольку у нас не будет прямого доступа к нему, единственный способ извлечь его — использовать .

      identity :: (a) -> a

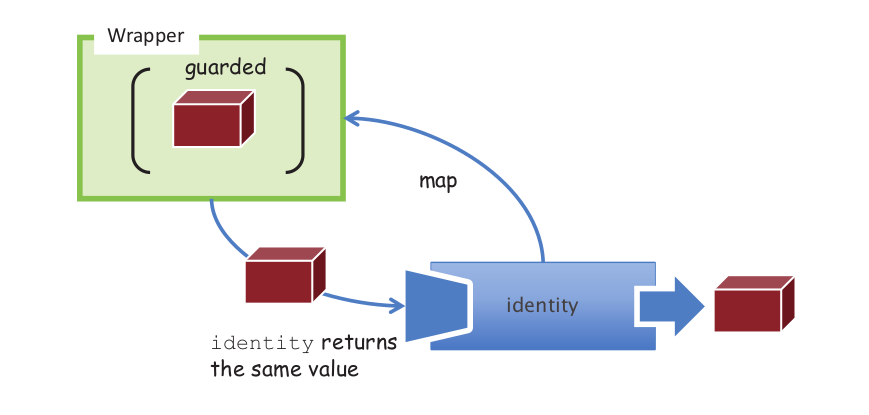
Это еще один пример использования функции идентификации: функциональное извлечение данных из инкапсулированных типов.

Тип Wrapper использует карту для безопасного доступа и управления значениями. В этом случае мы сопоставляем функцию идентификации с контейнером, чтобы извлечь значение из контейнера. При таком подходе мы можем проверять значение null перед вызовом функции или проверять наличие пустой строки, отрицательного числа и т. д.

       fmap :: (A -> B) -> Wrapper[A] -> Wrapper[B]

fmap сначала открывает контейнер, затем применяет данную функцию к его значению и, наконец, закрывает значение обратно в новый контейнер того же типа. Этот тип функции называется .

  • fmap возвращает новую копию контейнера при каждом вызове.

  • функторы не имеют побочных эффектов

  • функторы должны быть составными

Источник

На практике под функтором понимается объект, который реализует оператор вызова в C++. В ocaml я думаю, что functor относится к чему-то, что принимает модуль в качестве входного и выходного другого модуля.

Источник

Проще говоря, функтор или объект функции - это объект класса, который можно вызывать так же, как функцию.

В C++:

Вот как вы пишете функцию

void foo()
{
    cout << "Hello, world! I'm a function!";
}

Вот как ты пишешь функтор

class FunctorClass
{
    public:
    void operator ()
    {
        cout << "Hello, world! I'm a functor!";
    }
};

Теперь вы можете сделать это:

foo(); //result: Hello, World! I'm a function!

FunctorClass bar;
bar(); //result: Hello, World! I'm a functor!

Что делает их такими замечательными, так это то, что вы можете сохранять состояние в классе - представьте, хотите ли вы спросить функцию, сколько раз она была вызвана. Там нет никакого способа сделать это аккуратным, инкапсулированным способом. С функциональным объектом это так же, как и с любым другим классом: у вас будет некоторая переменная экземпляра, которую вы увеличиваете в operator () и какой-то метод для проверки этой переменной, и все аккуратно, как вам угодно.

Источник

Функтор конкретно не связан с функциональным программированием. Это просто "указатель" на функцию или какой-то объект, который может быть вызван как функция.

Источник
Другие вопросы по тегам