Несмещенный результат возвращает список из n случайных положительных чисел (>=0), так что их сумма == total_sum

Question

Я либо ищу алгоритм, либо предложение по улучшению моего кода для генерации списка случайных чисел, сумма которых равна некоторому произвольному числу. С моим кодом ниже, он всегда будет смещен, так как первые числа будут иметь тенденцию быть выше.

Есть ли способ сделать выбор номера более эффективным?

#!/usr/bin/python
'''
  Generate a list of 'numbs' positive random numbers whose sum = 'limit_sum'
'''

import random


def gen_list(numbs, limit_sum):
  my_sum = []
  for index in range(0, numbs):
    if index == numbs - 1:
      my_sum.append(limit_sum - sum(my_sum))
    else:
      my_sum.append(random.uniform(0, limit_sum - sum(my_sum)))

  return my_sum

#test
import pprint
pprint.pprint(gen_list(5, 20))
pprint.pprint(gen_list(10, 200))
pprint.pprint(gen_list(0, 30))
pprint.pprint(gen_list(1, 10))

ВЫХОД

## output

[0.10845093828525609,
 16.324799712999706,
 0.08200162072303821,
 3.4534885160590041,
 0.031259211932997744]

[133.19609626532952,
 47.464880208741029,
 8.556082341110228,
 5.7817325913462323,
 4.6342577008233716,
 0.22532341156764768,
 0.0027495225618908918,
 0.064738336208217895,
 0.028888697891734455,
 0.045250924420116689]

[]

[10]

Answer 1

Хорошо, мы собираемся решить эту проблему, предполагая, что необходимо сгенерировать случайный вектор длины N, который равномерно распределен по разрешенному пространству, пересчитанный следующим образом:

Дано

• желаемая длина L,
• желаемая общая сумма S,
• диапазон допустимых значений [0,B] для каждого скалярного значения,

генерировать случайный вектор V длины N таким образом, чтобы случайная величина V была равномерно распределена по ее разрешенному пространству.

---

Мы можем упростить задачу, отметив, что мы можем вычислить V = U * S, где U - подобный случайный вектор с желаемой общей суммой 1 и диапазоном допустимых значений [0,b], где b = B/S. Значение b должно быть между 1/N и 1.

---

Сначала рассмотрим N = 3. Пространство допустимых значений {U} - это часть плоскости, перпендикулярной вектору [1 1 1], которая проходит через точку [1/3 1/3 1/3] и которая лежит внутри куб, чьи компоненты находятся в диапазоне от 0 до b. Этот набор точек {U} имеет форму шестиугольника.

(TBD: изображение. Я не могу сгенерировать один прямо сейчас, мне нужен доступ к MATLAB или другой программе, которая может создавать 3D-графики. Моя установка Octave не может.)

Лучше всего использовать ортонормированную матрицу весов W (см. Мой другой ответ) с одним вектором = [1 1 1]/sqrt(3). Одна такая матрица

octave-3.2.3:1> A=1/sqrt(3)
   A =  0.57735
octave-3.2.3:2> K=1/sqrt(3)/(sqrt(3)-1)
   K =  0.78868
octave-3.2.3:3> W = [A A A; A 1-K -K; A -K 1-K]
   W =

     0.57735   0.57735   0.57735
     0.57735   0.21132  -0.78868
     0.57735  -0.78868   0.21132

который, опять же, ортонормирован (W*W = I)

Если вы рассмотрите точки куба [0 0 b],[0 b b],[0 b 0],[b b 0],[b 0 0] и [b 0 b], они образуют шестиугольник и все являются расстояние b*sqrt(2/3) от диагонали куба. Они не удовлетворяют рассматриваемой проблеме, но полезны через минуту. Две другие точки [0 0 0] и [b b b] находятся на диагонали куба.

Ортонормированная весовая матрица W позволяет нам генерировать точки, которые равномерно распределены в пределах {U}, потому что ортонормированные матрицы представляют собой преобразования координат, которые вращаются / отражаются и не масштабируются или наклоняются.

Мы будем генерировать точки, которые равномерно распределены в системе координат, определяемой 3 векторами W. Первый компонент - это ось диагонали куба. Сумма компонентов U полностью зависит от этой оси, а не от других. Поэтому координата вдоль этой оси должна быть равна 1/sqrt(3), что соответствует точке [1/3, 1/3, 1/3].

Два других компонента расположены в направлениях, перпендикулярных диагонали куба. Поскольку максимальное расстояние от диагонали составляет b*sqrt(2/3), мы будем генерировать равномерно распределенные числа (u,v) между -b*sqrt(2/3) и +b*sqrt(2/3).

Это дает нам случайную величину U' = [1/sqrt(3) u v]. Затем мы вычисляем U = U' * W. Некоторые из полученных точек будут за пределами допустимого диапазона (каждый компонент U должен быть между 0 и b), и в этом случае мы отклоняем это и начинаем заново.

Другими словами:

1. Генерация независимых случайных величин u и v, каждая из которых равномерно распределена между -b*sqrt(2/3) и +b*sqrt(3).
2. Вычислить вектор U '= [1/sqrt(3) uv]
3. Вычислить U = U' * W.
4. Если какой-либо из компонентов U находится за пределами диапазона [0,b], отклоните это значение и вернитесь к шагу 1.
5. Рассчитайте V = U * S.

---

Решение аналогично для более высоких измерений (равномерно распределенные точки в пределах части гиперплоскости, перпендикулярной главной диагонали гиперкуба):

Рассчитать весовую матрицу W ранга N.

1. Генерация независимых случайных величин u₁, u₂,... u_N-1, каждая из которых равномерно распределена между -b*k(N) и +b*k(N).
2. Вычислить вектор U '= [1/N u₁, u₂,... u_N-1]
3. Вычислите U = U' * W. (Существуют ярлыки для фактического построения и умножения на W.)
4. Если какой-либо из компонентов U находится за пределами диапазона [0,b], отклоните это значение и вернитесь к шагу 1.
5. Рассчитайте V = U * S.

Диапазон k (N) является функцией N, которая представляет максимальное расстояние вершин гиперкуба стороны 1 от его главной диагонали. Я не уверен в общей формуле, но это sqrt (2/3) для N = 3, sqrt(6/5) для N = 5, возможно, где-то есть формула для него.

Answer 2

Почему бы просто не генерировать правильное количество равномерно распределенных случайных чисел, не увеличивать их и не масштабировать?

РЕДАКТИРОВАТЬ: Чтобы быть немного яснее: вы хотите N чисел, которые в сумме S? Так что сгенерируйте N равномерно распределенных случайных чисел на интервале [0,1) или что бы ни генерировал ваш ГСЧ. Сложите их, они получат s (скажем), тогда как вы хотите, чтобы они составили S, поэтому умножьте каждое число на S/s. Теперь числа равномерно случайным образом распределены на [0,S/s), я думаю.

Answer 3

Вот как бы я это сделал:

1. Генерация n-1 случайных чисел, все в диапазоне [0,max]
2. Сортировать эти цифры
3. Для каждой пары, состоящей из i-го и (i+1)-го числа в отсортированном списке, создайте интервал (i,i+1) и вычислите его длину. Последний интервал начинается с последнего номера и заканчивается в max и первый интервал начинается с 0 и заканчивается первым номером в списке.

Теперь длины этих интервалов всегда будут составлять max, поскольку они просто представляют сегменты внутри [0,max].

Код (в Python):

#! /usr/bin/env python
import random

def random_numbers(n,sum_to):
    values=[0]+[random.randint(0,sum_to) for i in xrange(n-1)]+[sum_to]
    values.sort()
    intervals=[values[i+1]-values[i] for i in xrange(len(values)-1)]
    return intervals

if __name__=='__main__':
    print random_numbers(5,100)

Answer 4

Если вы ищете нормально распределенные числа с наименьшей корреляцией, насколько это возможно, и вам необходимо строго об этом *, я бы предложил вам воспользоваться следующим математическим подходом и перевести его на код.

(* строго: проблема с другими подходами заключается в том, что вы можете получить "длинные хвосты" в своих дистрибутивах - другими словами, редко, но возможно иметь выбросы, которые сильно отличаются от вашего ожидаемого результата)

• Сгенерируйте N-1 независимых и одинаково распределенных (IID) гауссовых случайных величин v₀, v₁, v₂,... v_N-1, чтобы соответствовать N-1 степеням свободы вашей задачи.
• Создайте вектор столбца V, где V = [0 v₀, v₁, v₂,... v_N-1]^T
• Используйте фиксированную весовую матрицу W, где W состоит из ортонормированной матрицы **, чья верхняя строка равна [1 1 1 1 1 1 1 ... 1] / sqrt(N).
• Ваш выходной вектор - это произведение WV + SU/N, где S - желаемая сумма, а U - вектор столбцов из 1. Другими словами, i-я выходная переменная = произведение точек (строка #i матрицы W) и вектор столбца V, добавленные к S/N.

Стандартное отклонение каждой выходной переменной будет (я полагаю, не могу проверить прямо сейчас) sqrt(N/N-1) * стандартное отклонение входных случайных величин.

** ортонормированная матрица: это сложная часть, я задаю вопрос на math.stackexchange.com, и есть простая матрица W, которая работает и может быть определена алгоритмически только с 3 различными значениями, так что на самом деле у вас нет построить матрицу.

W является отражением домохозяйства vw, где v = [sqrt(N), 0, 0, 0, ... ] и w = [1 1 1 1 1 ... 1] может быть определено как:

W(1,i) = W(i,1) = 1/sqrt(N)
W(i,i) = 1 - K   for i >= 2 
W(i,j) = -K      for i,j >= 2, i != j
K = 1/sqrt(N)/(sqrt(N)-1)

---

Проблема с подходом Марка:

Почему бы просто не генерировать правильное количество равномерно распределенных случайных чисел, не увеличивать их и не масштабировать?

в том, что если вы сделаете это, вы получите дистрибутив "длинный хвост". Вот пример в MATLAB:

 >> X = rand(100000,10);
 >> Y = X ./ repmat(sum(X,2),1,10);
 >> plot(sort(Y))

Я сгенерировал 100000 наборов из N=10 чисел в матрице X и создал матрицу Y, где каждая строка Y является соответствующей строкой X, разделенной на ее сумму (так, чтобы каждая строка Y суммировалась в 1,0)

Построение отсортированных значений Y (каждый столбец отсортирован отдельно) дает примерно одинаковое совокупное распределение:

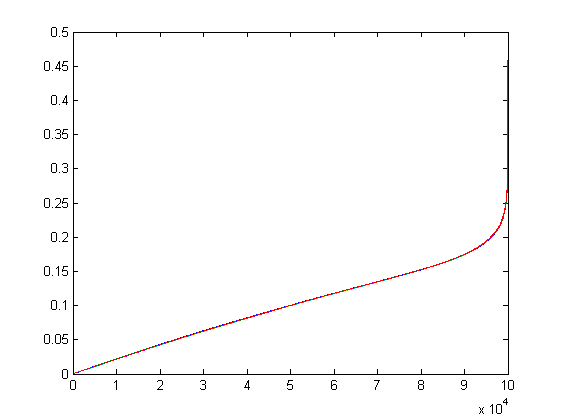
Истинное равномерное распределение даст прямую линию от 0 до максимального значения. Вы заметите, что это отчасти похоже на настоящее равномерное распределение, за исключением конца, где есть длинный хвост. Существует избыток чисел, генерируемых между 0,2 и 0,5. Хвост становится хуже при больших значениях N, потому что, хотя среднее значение чисел уменьшается (среднее = 1 / N), максимальное значение остается равным 1,0: вектор, состоящий из 9 значений 0,0 и 1 значения 1,0, действителен и может быть получен таким образом, но патологически редко.

Если вас это не волнует, используйте этот метод. И, вероятно, существуют способы генерирования "почти"-однородных или "почти" гауссовских распределений с желаемыми суммами, которые намного проще и эффективнее, чем те, которые я описал выше. Но я предупреждаю вас быть осторожным и понимать последствия выбранного вами алгоритма.

---

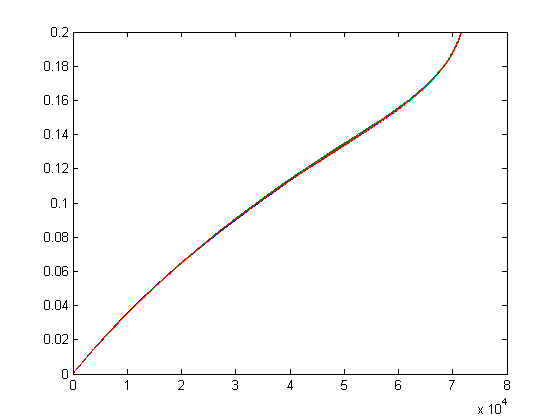
Одно исправление, которое оставляет вещи вроде равномерно распределенными без длинного хвоста, выглядит следующим образом:

1. Генерирует вектор V = N равномерно распределенных случайных чисел от 0,0 до 1,0.
2. Найдите их сумму S и их максимальное значение M.
3. Если S
4. Выведите вектор V*S по_{желанию}/S

Пример в MATLAB для N=10:

 >> X = rand(100000,10);
 >> Y = X ./ repmat(sum(X,2),1,10);
 >> i = sum(X,2)>(10/2)*max(X,[],2);
 >> plot(sort(Y(i,:)))

Answer 5

Я столкнулся с этой проблемой и специально нужны целые числа. Ответ заключается в использовании полинома.

import numpy.random, numpy
total_sum = 20
n = 6

v = numpy.random.multinomial(total_sum, numpy.ones(n)/n)

Как объясняет полиномиальная документация, вы бросали честные шестигранные кости двадцать раз. v содержит шесть чисел, указывающих количество раз, когда каждая сторона кости выпала. Естественно элементы v должны составить до двадцати. Здесь шесть n и двадцать total_sum,

С помощью многочлена вы можете также симулировать нечестные кости, что очень полезно в некоторых случаях.

Answer 6

Следующее довольно просто и возвращает единообразные результаты:

def gen_list(numbs, limit_sum):
    limits = sorted([random.uniform(0, limit_sum) for _ in xrange(numbs-1)])
    limits = [0] + limits + [limit_sum]
    return [x1-x0 for (x0, x1) in zip(limits[:-1], limits[1:])]

Идея состоит в том, что если вам нужно, скажем, 5 чисел от 0 до 20, вы можете просто поставить 4 "ограничения" между 0 и 20, и вы получите разбиение (0, 20) интервала. Случайные числа, которые вы хотите, это просто длина 5 интервалов в отсортированном списке [0, random1, random2, random3, random4, 20].

PS: ой! похоже, что это та же идея, что и ответ MAK, хотя и закодирован без использования индексов!

Answer 7

Вы можете сохранить промежуточный итог, а не звонить sum(my_sum) несколько раз.