Понимание свертки Scipy

Question

Я пытаюсь понять разницу между дискретной сверткой, предоставленной Сципи, и аналитическим результатом, который можно получить. Мой вопрос: как временная ось входного сигнала и функция отклика связаны с временной осью выходного сигнала дискретной свертки?

Чтобы попытаться ответить на этот вопрос, я рассмотрел пример с аналитическим результатом. Мой входной сигнал - гауссовский, а моя функция отклика - экспоненциальный спад с пошаговой функцией. Аналитические результаты свертки этих двух сигналов представляют собой модифицированный гауссов ( https://en.wikipedia.org/wiki/Exponentially_modified_Gaussian_distribution).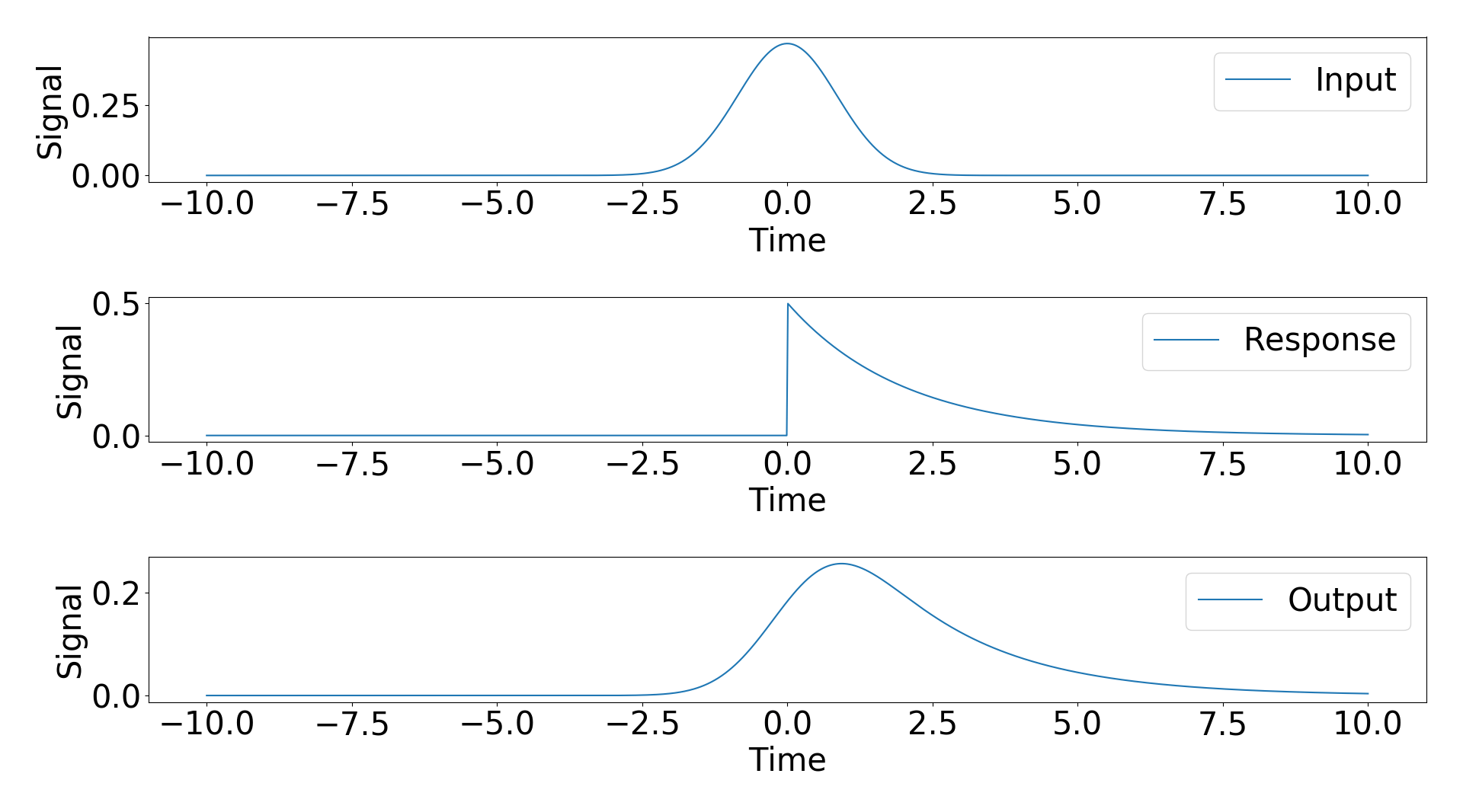

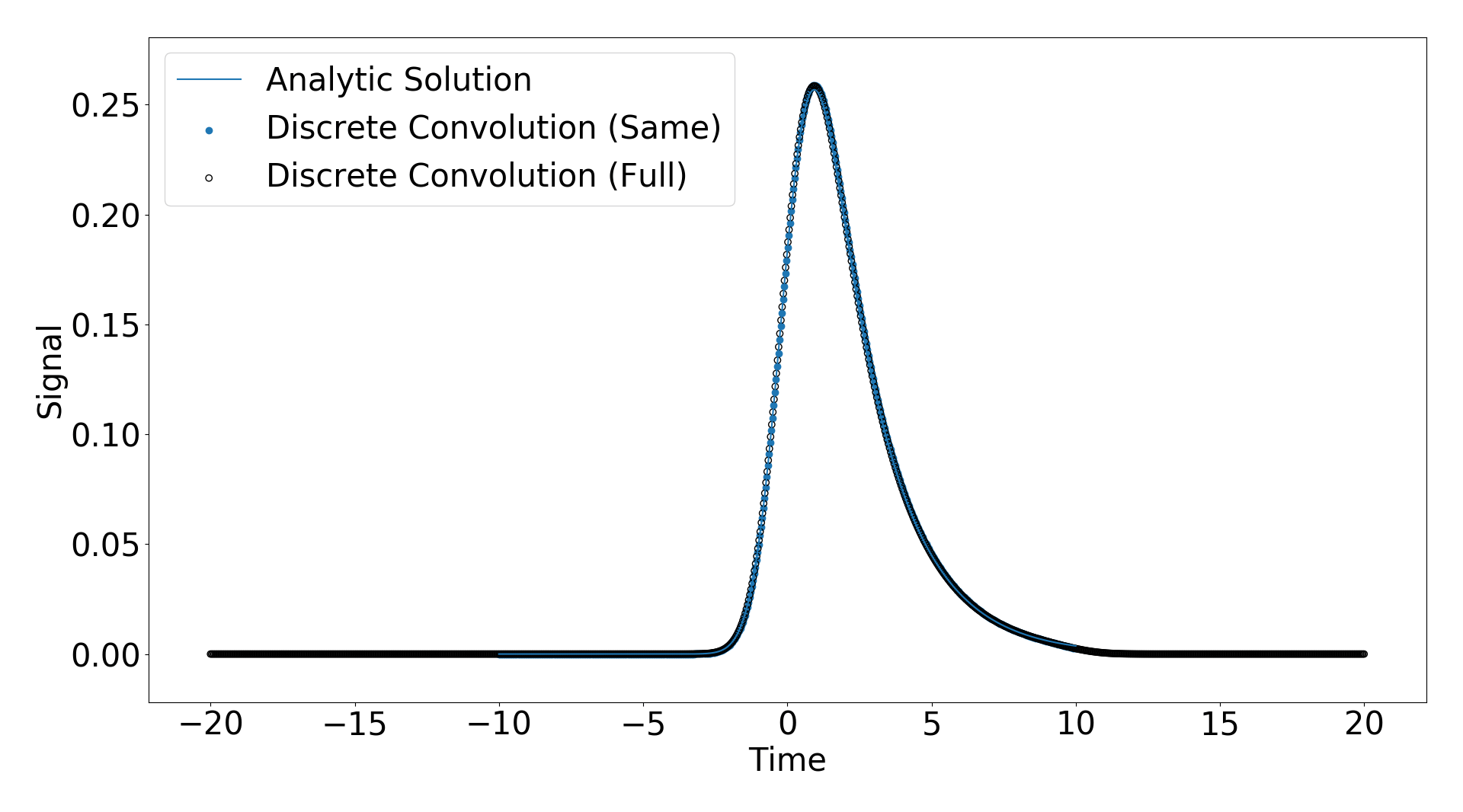
Сципи дает три режима свертки: "один и тот же", "полный", "действительный". Я применил "те же" и "полные" свертки и нанес результат на аналитическое решение ниже.

Вы можете видеть, что они соответствуют очень хорошо.

Одна важная особенность, которую следует отметить, состоит в том, что для "полной" дискретной свертки результирующая временная область намного больше, чем временная область входного сигнала (см. https://www.researchgate.net/post/How_can_I_get_the_convolution_of_two_signals_in_time_domain_by_just_having_the_values_of_amplitude_and_time_using_Matlab) Та же "дискретная свертка" у доменов времени одинакова и у доменов ввода и ответа (которые я выбрал, чтобы быть одинаковыми для этого примера).

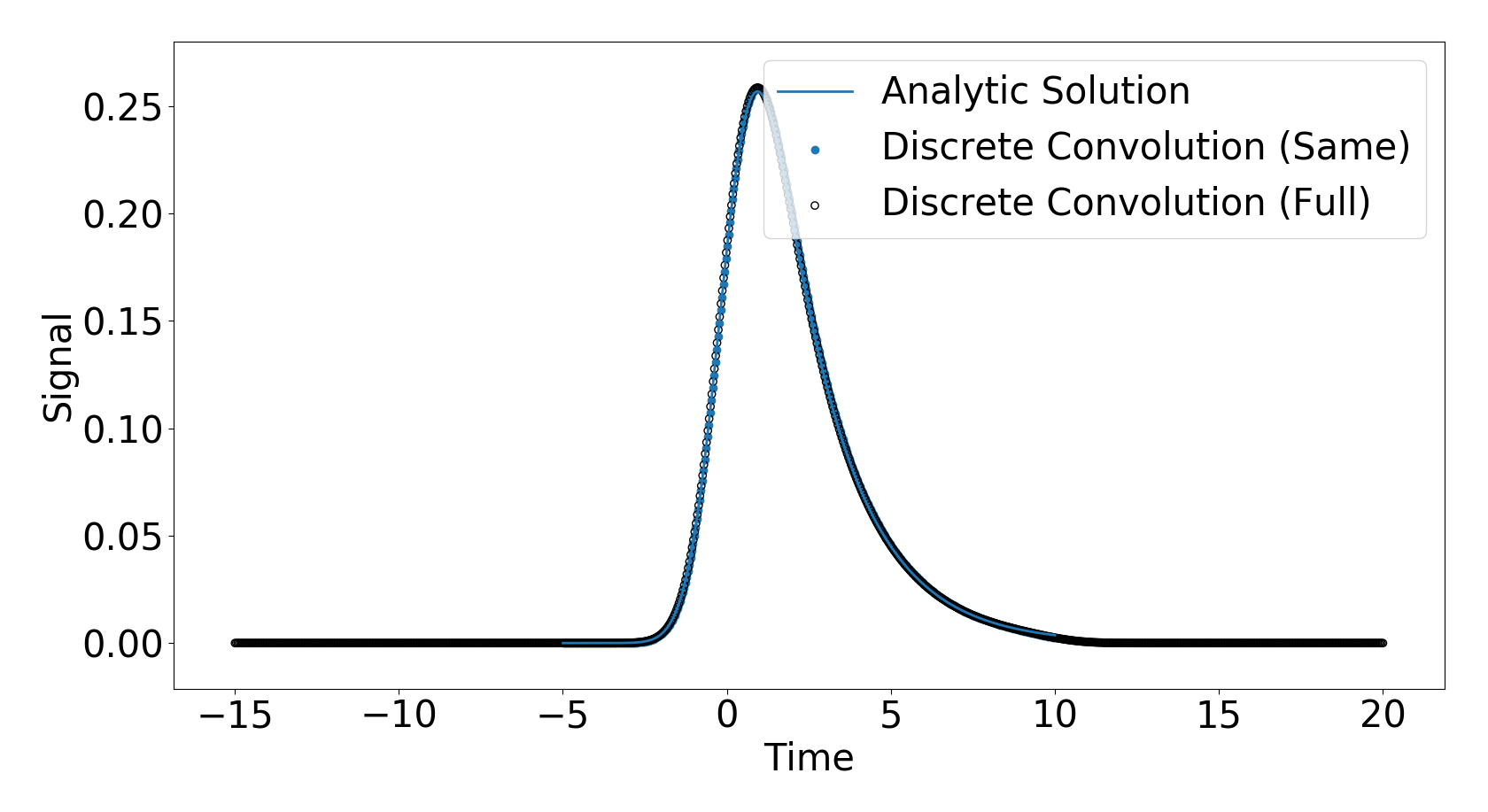
Моя путаница возникла, когда я заметил, что изменение области, в которой была заполнена моя функция ответа, изменило результат функций свертки. Это означает, что когда я установил t_response = np.linspace(-5,10,1000) вместо t_response = np.linspace(-10,10,1000) Я получил разные результаты, как показано ниже

Как видите, решения немного смещены. Мой вопрос: как временная ось входного сигнала и функция отклика связаны с временной осью выходного сигнала? Я приложил код, который я использую ниже, и любая помощь будет оценена.

import numpy as np
import matplotlib as mpl
from scipy.special import erf
import matplotlib.pyplot as plt
from scipy.signal import convolve as convolve
params = {'axes.labelsize': 30,'axes.titlesize':30, 'font.size': 30, 'legend.fontsize': 30, 'xtick.labelsize': 30, 'ytick.labelsize': 30}
mpl.rcParams.update(params)

def Gaussian(t,A,mu,sigma):
    return A/np.sqrt(2*np.pi*sigma**2)*np.exp(-(t-mu)**2/(2.*sigma**2))
def Decay(t,tau,t0):
    ''' Decay expoential and step function '''
    return 1./tau*np.exp(-t/tau) * 0.5*(np.sign(t-t0)+1.0)
def ModifiedGaussian(t,A,mu,sigma,tau):
        ''' Modified Gaussian function, meaning the result of convolving a gaussian with an expoential decay that starts at t=0'''
        x = 1./(2.*tau) * np.exp(.5*(sigma/tau)**2) * np.exp(- (t-mu)/tau)
        s = A*x*( 1. + erf(   (t-mu-sigma**2/tau)/np.sqrt(2*sigma**2)   ) )
        return s

### Input signal, response function, analytic solution
A,mu,sigma,tau,t0 = 1,0,2/2.344,2,0  # Choose some parameters for decay and gaussian
t = np.linspace(-10,10,1000)         # Time domain of signal
t_response = np.linspace(-5,10,1000)# Time domain of response function

### Populate input, response, and analyitic results
s = Gaussian(t,A,mu,sigma)
r = Decay(t_response,tau,t0)
m = ModifiedGaussian(t,A,mu,sigma,tau)

### Convolve
m_full = convolve(s,r,mode='full')
m_same = convolve(s,r,mode='same')
# m_valid = convolve(s,r,mode='valid')
### Define time of convolved data
t_full = np.linspace(t[0]+t_response[0],t[-1]+t_response[-1],len(m_full))
t_same = t
# t_valid = t

### Normalize the discrete convolutions
m_full /= np.trapz(m_full,x=t_full)
m_same /= np.trapz(m_same,x=t_same)
# m_valid /= np.trapz(m_valid,x=t_valid)

### Plot the input, repsonse function, and analytic result
f1,(ax1,ax2,ax3) = plt.subplots(nrows=3,ncols=1,num='Analytic')
ax1.plot(t,s,label='Input'),ax1.set_xlabel('Time'),ax1.set_ylabel('Signal'),ax1.legend()
ax2.plot(t_response,r,label='Response'),ax2.set_xlabel('Time'),ax2.set_ylabel('Signal'),ax2.legend()
ax3.plot(t_response,m,label='Output'),ax3.set_xlabel('Time'),ax3.set_ylabel('Signal'),ax3.legend()

### Plot the discrete  convolution agains analytic
f2,ax4 = plt.subplots(nrows=1)
ax4.scatter(t_same[::2],m_same[::2],label='Discrete Convolution (Same)')
ax4.scatter(t_full[::2],m_full[::2],label='Discrete Convolution (Full)',facecolors='none',edgecolors='k')
# ax4.scatter(t_valid[::2],m_valid[::2],label='Discrete Convolution (Valid)',facecolors='none',edgecolors='r')
ax4.plot(t,m,label='Analytic Solution'),ax4.set_xlabel('Time'),ax4.set_ylabel('Signal'),ax4.legend()
plt.show()

Answer 1

Суть проблемы в том, что в первом случае ваши сигналы имеют одинаковую частоту дискретизации, а во втором - нет.

Я чувствую, что об этом легче думать в частотной области, где свертка - это умножение. Когда вы создаете сигнал и фильтр с одинаковой временной осью, np.linspace(-10, 10, 1000)Теперь они имеют одинаковую частоту дискретизации. Применяя преобразование Фурье к каждому, полученные массивы дают мощность на тех же частотах для сигнала и фильтра. Таким образом, вы можете напрямую умножить соответствующие элементы этих массивов.

Но когда вы создаете сигнал с временной осью np.linspace(-10, 10, 1000) и фильтр с временной осью np.linspace(-5, 10, 1000), это больше не правда. Применение преобразования Фурье и умножение соответствующих элементов больше не является правильным, потому что частоты в соответствующих элементах не совпадают.

Давайте сделаем это конкретно, используя ваш пример. Частота первого элемента преобразования (т. Е. np.fft.fftfreq(1000, np.diff(t).mean())[1]) сигнала (s) около 0.05 Hz, Но для фильтра (r) частота первого элемента составляет около 0.066 Hz, Таким образом, умножение этих двух элементов умножает мощность на двух разных частотах. (Из-за этой тонкости вы часто видите примеры обработки сигналов, в которых сначала определяется частота дискретизации, а затем создаются временные массивы, сигналы и фильтры на основе этого.)

Вы можете убедиться, что это правильно, создав фильтр, который распространяется на интересующий вас диапазон времени. [-5, 10), но с той же частотой дискретизации, что и исходный сигнал. Итак, используя:

t = np.linspace(-10, 10, 1000)
t_response = t[t > -5.0]

генерирует сигнал и фильтрует в разных временных диапазонах, но с одинаковой частотой дискретизации, поэтому свертка должна быть правильной. Это также означает, что вам нужно изменить способ построения каждого массива. Код должен быть:

ax4.scatter(t_response[::2], m_same[125:-125:2], label='Same') # Conv extends beyond by ((N - M) / 2) == 250 / 2 == 125 on each side
ax4.scatter(t_full[::2], m_full[::2], label='Full')
ax4.scatter(t_response, m, label='Analytic solution')

Это создает график ниже, в котором аналитические, полные и те же свертки хорошо совпадают.