Полоска Scipy Butter не дает желаемых результатов
Поэтому я пытаюсь пропустить 24-битный файл 44,1 кГц в формате wav PCM. То, что я хотел бы сделать, это полоса пропускания каждой частоты от 0 Гц до 22 кГц.
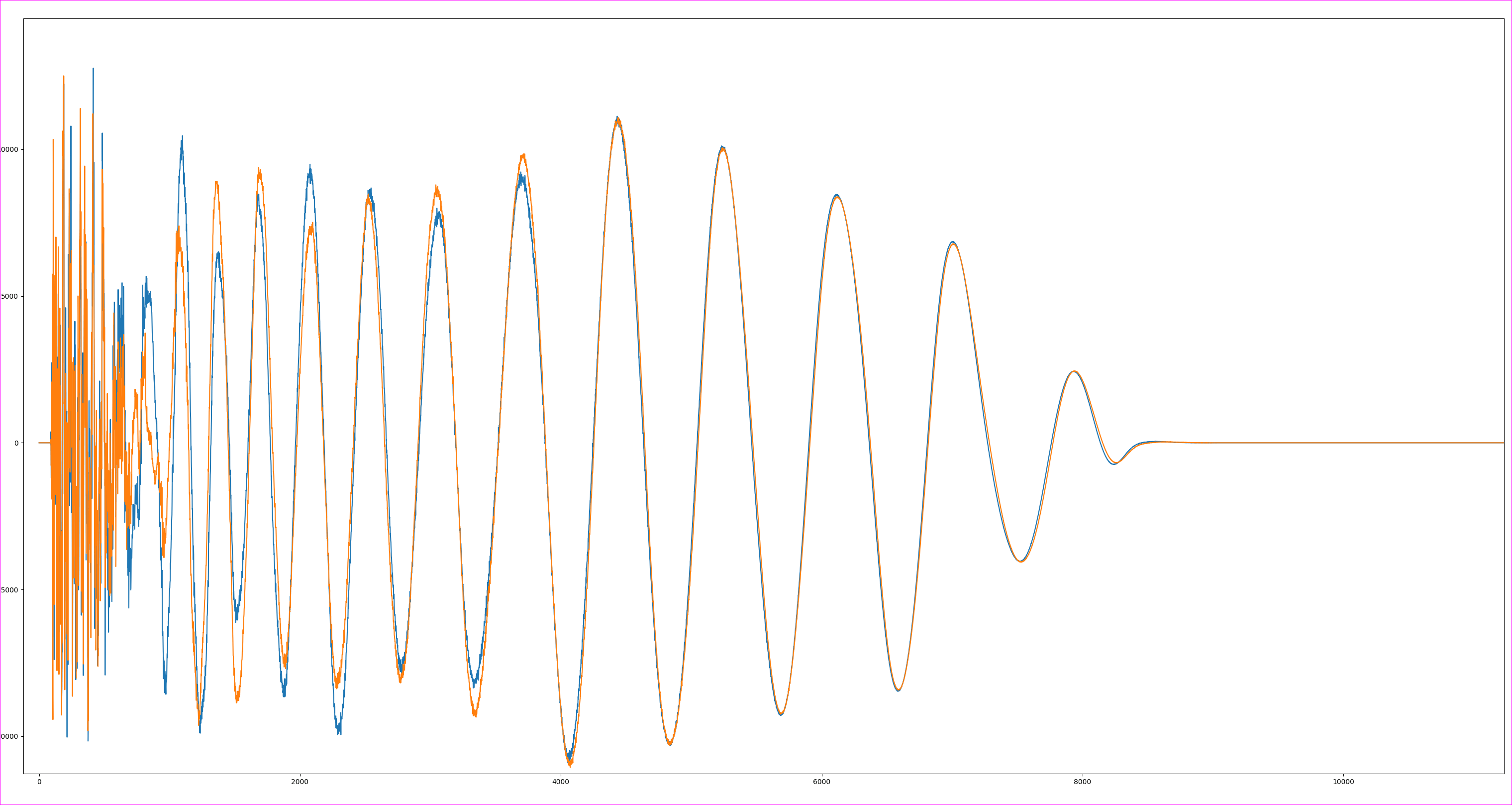
Пока я загрузил данные и могу отобразить их на Matplot, и это выглядит следующим образом.
Но когда я иду применить полосовой фильтр, который я получил отсюда
http://scipy-cookbook.readthedocs.io/items/ButterworthBandpass.html
Я получаю следующий результат: 
Поэтому я пытаюсь в качестве теста пропускать 100-101 Гц, вот мой код:
from WaveData import WaveData
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter, freqz
from scipy.io.wavfile import read
import numpy as np
from WaveData import WaveData
class Filter:
def __init__(self, wav):
self.waveData = WaveData(wav)
def butter_bandpass(self, lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(self, data, lowcut, highcut, fs, order):
b, a = self.butter_bandpass(lowcut, highcut, fs, order=order)
y = lfilter(b, a, data)
return y
def getFilteredSignal(self, freq):
return self.butter_bandpass_filter(data=self.waveData.file['Data'], lowcut=100, highcut=101, fs=44100, order=3)
def getUnprocessedData(self):
return self.waveData.file['Data']
def plot(self, signalA, signalB=None):
plt.plot(signalA)
if signalB != None:
plt.plot(signalB)
plt.show()
if __name__ == "__main__":
# file = WaveData("kick.wav")
# fileA = read("kick0.wav")
f = Filter("kick.wav")
a, b = f. butter_bandpass(lowcut=100, highcut=101, fs=44100)
w, h = freqz(b, a, worN=22000) ##Filted signal is not working?
f.plot(h, w)
print("break")
Я не понимаю, где я ошибся.
Спасибо
2 ответа
То, что сказал @WoodyDev, верно: 1 Гц из 44,1 кГц - это слишком малая полоса пропускания для любого типа фильтра. Просто посмотрите на коэффициенты фильтра butter возвращает:
In [3]: butter(5, [100/(44.1e3/2), 101/(44.1e3/2)], btype='band')
Out[3]:
(array([ 1.83424060e-21, 0.00000000e+00, -9.17120299e-21, 0.00000000e+00,
1.83424060e-20, 0.00000000e+00, -1.83424060e-20, 0.00000000e+00,
9.17120299e-21, 0.00000000e+00, -1.83424060e-21]),
array([ 1. , -9.99851389, 44.98765092, -119.95470631,
209.90388506, -251.87018009, 209.88453023, -119.93258575,
44.9752074 , -9.99482662, 0.99953904]))
Посмотрите на b Коэффициенты (первый массив): их значения в 1e-20, что означает, что конструкция фильтра полностью не сходится, и если вы примените его к любому сигналу, выходной сигнал будет равен нулю - что вы и нашли.
Вы не упомянули свое приложение, но если вы действительно хотите сохранить частотный контент сигнала между 100 и 101 Гц, вы можете взять FFT сигнала с добавлением нуля, обнулить части спектра за пределами этой полосы и IFFT (посмотри на rfft, irfft, а также rfftfreq в numpy.fft модуль).
Вот функция, которая применяет полосовой фильтр с кирпичной стенкой в области Фурье с использованием БПФ:
import numpy.fft as fft
import numpy as np
def fftBandpass(x, low, high, fs=1.0):
"""
Apply a bandpass signal via FFTs.
Parameters
----------
x : array_like
Input signal vector. Assumed to be real-only.
low : float
Lower bound of the passband in Hertz. (If less than or equal
to zero, a high-pass filter is applied.)
high : float
Upper bound of the passband, Hertz.
fs : float
Sample rate in units of samples per second. If `high > fs / 2`,
the output is low-pass filtered.
Returns
-------
y : ndarray
Output signal vector with all frequencies outside the `[low, high]`
passband zeroed.
Caveat
------
Note that the energe in `y` will be lower than the energy in `x`, i.e.,
`sum(abs(y)) < sum(abs(x))`.
"""
xf = fft.rfft(x)
f = fft.rfftfreq(len(x), d=1 / fs)
xf[f < low] = 0
xf[f > high] = 0
return fft.irfft(xf, len(x))
if __name__ == '__main__':
fs = 44.1e3
N = int(fs)
x = np.random.randn(N)
t = np.arange(N) / fs
import pylab as plt
plt.figure()
plt.plot(t, x, t, 100 * fftBandpass(x, 100, 101, fs=fs))
plt.xlabel('time (seconds)')
plt.ylabel('signal')
plt.legend(['original', 'scaled bandpassed'])
plt.show()
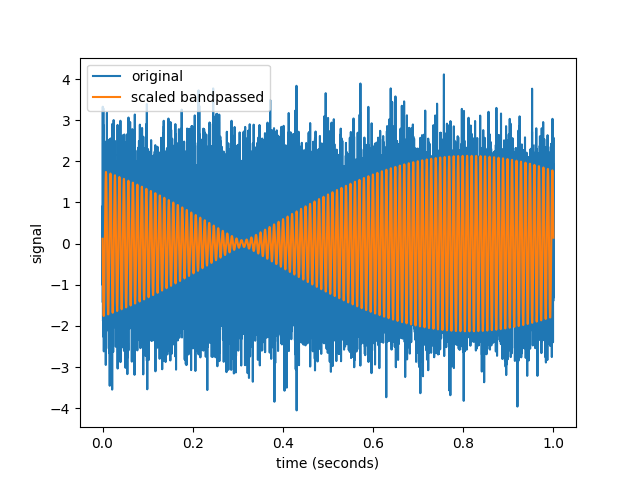
Вы можете поместить это в файл, fftBandpass.py и просто запустить его с python fftBandpass.py чтобы увидеть его, создайте следующий сюжет:
Заметьте, мне пришлось масштабировать полосовой сигнал с частотой 1 Гц на 100, потому что после такой пропускной полосы в сигнале очень мало энергии. Также обратите внимание, что сигнал, живущий в этой небольшой полосе пропускания, представляет собой синусоиду с частотой около 100 Гц.
Если вы добавите следующее в свой собственный код: from fftBandpass import fftBandpass, вы можете использовать fftBandpass функция.
Еще одна вещь, которую вы можете попробовать - это уменьшить сигнал в 100 раз, поэтому преобразуйте его в сигнал с частотой 441 Гц.1 Гц из 441 Гц по-прежнему является узкополосной полосой пропускания, но вам, возможно, повезет больше, чем попытаться пропустить исходный сигнал. Увидеть scipy.signal.decimate, но не пытайтесь назвать это с q=100 вместо рекурсивного прореживания сигнала, 2, затем 2, затем 5, затем 5 (для полного прореживания 100x).
Так что с вашим кодом есть некоторые проблемы, которые означают, что вы не правильно отображаете результаты, хотя я считаю, что это не ваша главная проблема.
Проверьте свой код
В приведенном вами примере они точно показывают процесс расчета и построения фильтра для разных порядков:
for order in [3, 6, 9]:
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
w, h = freqz(b, a, worN=2000)
plt.plot((fs * 0.5 / np.pi) * w, abs(h), label="order = %d" % order)
В настоящее время вы неправильно масштабируете свою ось частоты или вызываете абсолютное значение, чтобы получить реальную информацию от h, как правильный код выше.
Проверь свою теорию
Тем не менее, ваша главная проблема, это ваш такой крутой диапазон (то есть только 100 Гц - 101 Гц). Очень редко я видел такой резкий фильтр, так как он очень интенсивно обрабатывает (потребует много коэффициентов фильтра), и, поскольку вы смотрите только в диапазоне 1 Гц, он полностью избавится от всех других частот.
Так что график, который вы показали с коэффициентом усиления 0, вполне может быть правильным. Если вы используете их пример и измените частоты среза полосы пропускания на 100 Гц -> 101 Гц, то выходной результат будет массивом (почти, если не полностью) нулей. Это потому, что он будет смотреть только на энергию сигнала в диапазоне 1 Гц, который будет очень очень мал, если вы подумаете об этом.
Если вы делаете это для анализа, частотный интервал имеет тенденцию быть намного большим, то есть октавные полосы (или меньшие деления октавных полос).
Спектрограмма
Поскольку я не уверен в вашей конечной цели, я не могу уточнить, по какому маршруту вы должны идти, чтобы туда добраться. Однако использование полосовых фильтров на каждой частоте до 20 кГц кажется глупым в наше время.
Если я правильно помню, некоторые из первых попыток спектрограммы с иглами на бумаге использовали эту технику с банками аналоговых полосовых фильтров для анализа частотного содержимого. Так что это заставляет меня думать, что вы, возможно, ищете что-то, связанное со спектрограммой? Он позволяет вам анализировать информацию о частоте всего сигнала в зависимости от времени и по-прежнему содержит всю информацию об амплитуде сигнала. Python уже имеет функциональность спектрограммы, включенную как часть scipy или Matplotlib.