Если для дерева решений выбран плохой атрибут, есть ли здесь последовательная гипотеза?

Question

Я взял предложение из записки кому-то, и теперь мне интересно, как это утверждение может быть действительным:

При построении дерева решений для данных без шума, если для root не была выбрана хорошая функция, мы все равно можем создать непротиворечивую гипотезу.

Это не имеет смысла для меня: почему мы все еще можем создать последовательное дерево решений в этом состоянии?

Примечание: если f является целевой функцией, мы говорим, гипотеза h согласуется, если он согласен с f на всех примерах

Answer 1

Если бы я не понял вопрос неправильно, я бы сказал, что это утверждение верно.

Это не самая простая вещь, чтобы привести быстрый пример, но вот он (извините за мои плохие навыки рисования).

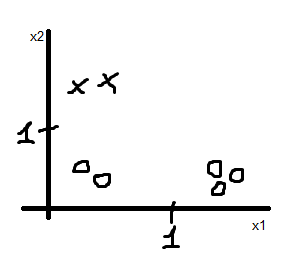
На этом рисунке мы видим, как выбрать в качестве корневого элемента функцию x2 возвращает максимальный прирост информации и позволяет нам найти непротиворечивую гипотезу с минимальным деревом решений. по факту h(x) = "cross" если x2 > 1,

Это не мешает нам найти последовательную гипотезу, выбирающую худшую особенность, x1, как корень. Пройдя по этому пути, мы получили бы начальное ветвление x1:

x1 < 1 отсюда мы бы затем выполнить последовательное ветвление x2

x1 > 1 и отсюда то же самое.

Таким образом, мы получили бы h(x) = "cross" если x1 < 1 && x2 > 1, h(x) = "circle" иначе. Таким образом, последовательная гипотеза снова.