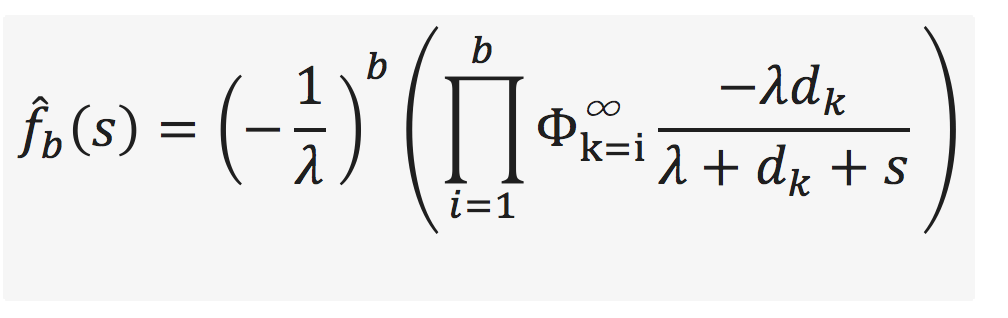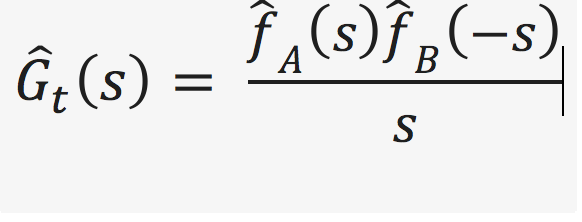Обратное преобразование Лапласа обобщенных цепных дробей с использованием Python, Sympy

Question

Как следует из названия, я пытаюсь реализовать вышеизложенное. Моя первая попытка сделать это заключалась в решении части непрерывной дроби. Вопрос: Как я узнаю, насколько глубоко мне нужно углубиться в продолжение дробной части? Я попытался выбрать 3 уровня (продолжение фракции, которая опускается на 3 уровня). Но для этого требуется много времени. Может кто-нибудь, пожалуйста, помогите? Вот мой код:

Моя функция, которая вычисляет обобщенную цепную дробь:

def list_to_fract2(l,l2):
    expr2 = sym.Integer(0)
    for i,j in zip(reversed(l),reversed(l2)):
        expr2 = j-expr2
        expr1 = i
        expr2 = expr1 / expr2
    return expr2

ak = sym.symbols("a1:4") #3 levels deep
bk = sym.symbols('b1:4') #3 levels deep
mu = sym.Symbol('mu')
s,lam = sym.symbols(['s','lam'])

expr = list_to_fract2(ak,bk) 

expr

a1 / (- a2 / (- a3 / b3 + b2) + b1)

#Initializing parameters to be subbed into sympy later
k = np.arange(1,len(ak)+1)
dk = mu + k*frac(str(thetas[0]))
a_k = lam * dk
b_k = s + dk + lam
expr = expr.subs({i:j for i,j in zip(ak,a_k)})
expr

lam *(mu + 71/100) / (b1 - lam *(mu + 71/50) / (b2 - lam *(mu + 213/100) / b3))

expr = expr.subs({i:j for i,j in zip(bk,b_k)})
expr

лам *(му + 71/100)/(- лам *(му + 71/50)/(- лам *(му + 213/100)/(лам + му + с + 213/100) + лам + му + s + 71/50) + lam + mu + s + 71/100)

expr = expr.subs({'mu': frac(str(mu2)),'lam':frac(str(lamda_emp[0]))})
expr

1221 / (400 *(с + 7/2 - 2183/(500*(с + 421/100 - 11359/(2000*(с + 123/25))))))

Вопрос: теперь это то, что я должен взять обратно?

Затем я попробовал это:

t = sym.symbols("t", positive=True)
ans = sym.inverse_laplace_transform(expr,s,t).evalf().simplify()

Это занимает слишком много времени, чтобы выполнить в моей машине. Если я изменю уровни на 2, то в этом случае он на самом деле работает довольно быстро. Может кто-нибудь помочь с этим? Спасибо

Мои параметры следующие: му = 0,94, тета = 0,71, лямда = 1,85

дк = к * тета

ак = лам * дк

bk = s + dk + lam

Я пытаюсь решить следующую функцию. Предположим, что b = 1 в простом случае. И, наконец, принимая обратное преобразование Лапласа этого

На самом деле, я хочу взять обратный знак из следующего уравнения. Но прежде чем я попробую это, я хотел сначала попробовать для базового случая.