Преобразование Баттерворта 2-го порядка в 1-й порядок - Часть II -

Question

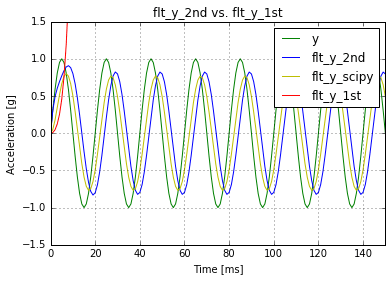
Я пытаюсь преобразовать мой рабочий фильтр низких частот Баттерворта 2-го порядка в 1-й порядок в Python, но он дает мне очень большие числа, например flt_y_1st[299]: 26198491071387576370322954146679741443295686950912.0. Вот мой Баттерворт 2-го и 1-го порядка:

import math
import numpy as np
import matplotlib.pyplot as plt

from scipy.signal import lfilter
from scipy.signal import butter

def butter_lowpass(cutoff, fs, order=1):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def butter_lowpass_filter(data, cutoff, fs, order=1):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y

def bw_2nd(y, fc, fs):
    filtered_y = np.zeros(len(y))

    omega_c = math.tan(np.pi*fc/fs)
    k1 = np.sqrt(2)*omega_c
    k2 = omega_c**2
    a0 = k2/(1+k1+k2)
    a1 = 2*a0
    a2 = a0
    k3 = 2*a0/k2
    b1 = -(-2*a0+k3)
    b2 = -(1-2*a0-k3)

    filtered_y[0] = y[0]
    filtered_y[1] = y[1]

    for i in range(2, len(y)):
        filtered_y[i] = a0*y[i]+a1*y[i-1]+a2*y[i-2]-(b1*filtered_y[i-1]+b2*filtered_y[i-2])

    return filtered_y


def bw_1st(y, fc, fs):
    filtered_y = np.zeros(len(y))

    omega_c = math.tan(np.pi*fc/fs)
    k1 = np.sqrt(2)*omega_c
    k2 = omega_c**2
    a0 = k2/(1+k1+k2)
    a1 = 2*a0
    k3 = 2*a0/k2
    b1 = -(-2*a0+k3)
#    b1 = -(-2*a0)  # <= Removing k3 makes better, but still not perfect

    filtered_y[0] = y[0]

    for i in range(1, len(y)):
       filtered_y[i] = a0*y[i]+a1*y[i-1]-(b1*filtered_y[i-1])

    return filtered_y

f = 100
fs = 2000
x = np.arange(300)
y = np.sin(2 * np.pi * f * x / fs)

flt_y_2nd = bw_2nd(y, 120, 2000)
flt_y_scipy = butter_lowpass_filter(y, 120, 2000, 1)
flt_y_1st = bw_1st(y, 120, 2000)

for i in x:
    print('y[%d]: %6.3f flt_y_2nd[%d]: %6.3f flt_y_scipy[%d]: %6.3f flt_y_1st[%d]: %8.5f' % (i, y[i], i, flt_y_2nd[i], i, flt_y_scipy[i], i, flt_y_1st[i]))

plt.subplot(1, 1, 1)
plt.xlabel('Time [ms]')
plt.ylabel('Acceleration [g]')
lines = plt.plot(x, y, x, flt_y_2nd, x, flt_y_scipy, x, flt_y_1st)
l1, l2, l3, l4 = lines
plt.setp(l1, linewidth=1, color='g', linestyle='-')
plt.setp(l2, linewidth=1, color='b', linestyle='-')
plt.setp(l3, linewidth=1, color='y', linestyle='-')
plt.setp(l4, linewidth=1, color='r', linestyle='-')
plt.legend(["y", "flt_y_2nd", "flt_y_scipy", "flt_y_1st"])
plt.grid(True)
plt.xlim(0, 150)
plt.ylim(-1.5, 1.5)
plt.title('flt_y_2nd vs. flt_y_scipy vs. flt_y_1st')
plt.show()

... Я удалил все [i-2], которые были прямой и обратной.

Однако, кажется, этого недостаточно. Я думаю, что мне нужно изменить некоторые уравнения в a0, b1 и т. Д. Например, когда я удаляю '+k3' из b1, я получаю график вроде этого (выглядит лучше, не так ли?):

Я не специализируюсь на фильтрах, но, по крайней мере, я знаю, что этот 1-й порядок отличается от порядка scipy.butter. Поэтому, пожалуйста, помогите мне найти правильные коэффициенты. Заранее спасибо.

Вот моя ссылка: filtering_considerations.pdf

Answer 1

Позвольте мне ответить самому себе.

Конечные коэффициенты:

omega_c = math.tan(np.pi*fc/fs)
k1 = np.sqrt(2)*omega_c
a0 = k1/(math.sqrt(2)+k1)
a1 = a0
b1 = -(1-2*a0)

Вот как. Я перепроектировал их из scipy.butter, как предложил @sizzzzlerz (спасибо). scipy.butter выплевывает эти коэффициенты:

b:  [ 0.16020035  0.16020035]
a:  [ 1.        -0.6795993]

Обратите внимание, что б и а обратные от моей ссылки. Они будут:

a0 = 0.16020035
a1 = 0.16020035
b0 = 1
b1 = -0.6795993

Затем применили эти коэффициенты к моей неполной формуле:

a1 = a0 = 0.16020035
b1 = -(1-2*a0) = -{1-2*(0.16020035)} = -(0.6795993)

Все идет нормально. Кстати:

k1 = 0.2698
k2 = 0.0364

Так:

a0 = k2/(1+k1+k2) = 0.0364/(1+0.2698+0.0364) = 0.0279

... Это далеко от 0.16020035. На этом этапе я исключил k2 и поставил так:

a0 = k1/(1+k1+x)

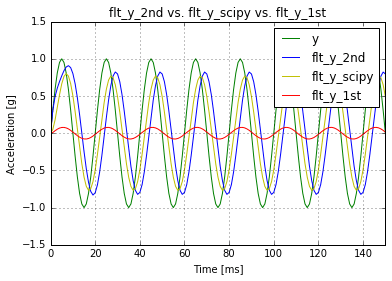
Когда х = 0,4142, я получил 0,16020164. Достаточно близко.

a0 = k1/(1+k1+0.4142) = k1/(1.4142+k1)

... 1.4142...!? Я когда-либо видел этот номер раньше...:

= k1/(math.sqrt(2)+k1)

Теперь график выглядит следующим образом (flt_y_scipy полностью покрывается flt_y_1st):

Вы можете искать по ключевым словам "первый заказ" butterworth "фильтр нижних частот" "sqrt(2)" и т. Д.

Это конец моего воскресного DIY.;-)