Линия, которая вызывает наихудший случай для алгоритма Дугласа-Пейкера?

Question

Алгоритм упрощения линии Дугласа-Пекера имеет наихудшую временную сложность O(n²). Однако для того, чтобы строка фактически запустила этот наихудший случай, две вещи должны идти "неправильно" одновременно:

• порог должен быть установлен так низко, что большинство вершин сохраняются
• на каждом шаге рекурсии вершина с наибольшим отклонением от линии между текущими конечными точками должна быть близка (с точки зрения ее индекса на линии, а не с точки зрения ее евклидова позиции) к одной из конечных точек. (Если вместо этого индекс вершины с наибольшим отклонением от линии находился достаточно близко к середине между текущими конечными точками, алгоритм должен вызывать рекурсивное двоичное подразделение глубины log(n), что приводит к общей сложности времени O(n log(n)).)

Хотя первый критерий легко вызвать (просто установите порог допуска на 0,0), я еще не нашел линию, которая удовлетворяет второму критерию.

Таким образом, есть простая примерная линия, которая приводит к поведению в наихудшем случае (предпочтительно та, которая запускает очевидный наихудший случай, когда точка с наибольшим отклонением на каждом этапе рекурсии напрямую связана с одной из конечных точек линии; но любой другой пример тоже хорошо)?

Answer 1

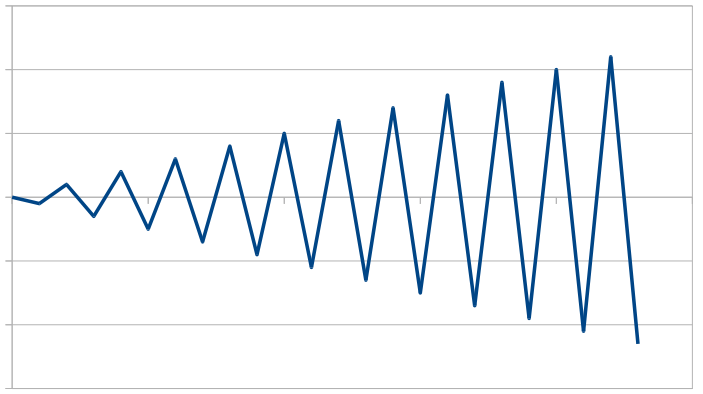
Так что Винсент ван дер Уил, похоже, прав: простая зигзагообразная линия с возрастающей амплитудой вызовет наихудший случай O(n²) для алгоритма Дугласа-Пекера:

В этом случае вершина с самым длинным расстоянием от линии, соединяющей две конечные точки, всегда будет той, которая непосредственно примыкает к конечной точке справа. Таким образом, алгоритм Дугласа-Пейкера здесь потребует O(n) шагов подразделения, где каждый шаг просто сбривает самую правую вершину и, следовательно, должен перебрать оставшиеся O(n) вершины, чтобы найти ту, которая имеет наибольшее расстояние - давая общая сложность времени O(n²)