Почему PyBrain не может изучать бинарный файл

Question

Я пытаюсь получить сеть (PyBrain) для изучения двоичного файла. Это мой код, и он сохраняет возвращаемые значения около 8, но он должен быть возвращен 9, когда я активируюсь с этой целью.

from pybrain.tools.shortcuts import buildNetwork
from pybrain.structure import *
from pybrain.datasets import *
from pybrain.supervised.trainers import BackpropTrainer
from matplotlib.pyplot import *


trains = 3000
hiddenLayers = 4
dim = 4
target = (1, 0, 0, 1)

ds = SupervisedDataSet(dim, 1)

ds.addSample((0, 0, 0, 0), (0,))
ds.addSample((0, 0, 0, 1), (1,))
ds.addSample((0, 0, 1, 0), (2,))
ds.addSample((0, 0, 1, 1), (3,))
ds.addSample((0, 1, 0, 0), (4,))
ds.addSample((0, 1, 0, 1), (5,))
ds.addSample((0, 1, 1, 0), (6,))
ds.addSample((0, 1, 1, 1), (7,))
ds.addSample((1, 0, 0, 0), (8,))


net = buildNetwork(dim, hiddenLayers, 1, bias=True, hiddenclass=SigmoidLayer)
trainer = BackpropTrainer(net, ds)

tests = []

for i in range(trains):
    trainer.train()
    tests.append(net.activate(target))


plot(range(len(tests)), tests)


print net.activate(target)
show()

Я попытался настроить количество скрытых слоев, скрытый класс от TanhLayer до SigmoidLayer и изменил количество поездов, но оно всегда сходится примерно в 500 раз (обучая сеть к набору данных). Должен ли я использовать другой тренажер, чем обратное распространение, и если да, то почему?

Answer 1

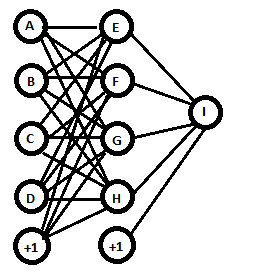
Вы создали сеть с 4 входными узлами, 4 скрытыми узлами, 1 выходным узлом и 2 смещениями.

Рассматривая каждую букву как активацию для этого узла, мы можем сказать, что каждый скрытый узел вычисляет свою активацию как сигмоид (w₀* 1 + w₁* A + w₂* B + w₃* C + w₄* D), и Выходной узел вычисляет свою активацию как (w₀* 1 + w₁* E + w₂* F + w₃* G + w₄* H) (без сигмоида). Количество линий на диаграмме - это количество весовых параметров в модели, которые были изменены в процессе обучения.

Имея так много параметров и только 9 выборок для обучения, существует множество локально оптимальных, не совсем правильных решений, к которым может сходиться сеть.

Один из способов исправить это - увеличить количество тренировочных образцов. Вы можете обобщить последние 1 и 0 и предложить выборки, такие как ((0, 0, 1,0, 0,5), (2,5,)) и ((0, 1,2, 0,0, 1,0), (5,8,)).

Другой вариант - упростить вашу модель. Все, что вам нужно для идеального решения, - это 4 входа, подключенных непосредственно к выходу без смещений или сигмоидов. Эта модель будет иметь только 4 весовых коэффициента, для обучения которых будет установлено значение 1, 2, 4 и 8. Окончательное вычисление будет 1*A + 2*B + 4*C + 8*D.

Answer 2

Я бы посоветовал вам сделать цель чем-то посередине, а не на краю.

Я попытался расширить тренировочные данные вверх на 10 и 11, тогда это дало лучшие результаты при прогнозировании 9, даже если 9 пропущено из тренировочных данных. Также вы получите довольно хороший результат, если попытаетесь предсказать 4, даже если у вас нет 4 в данных тренировки.

Исходя из моего опыта, я не ожидал, что нейронная сеть будет легко угадывать числа, выходящие за границы тестовых данных.