Восстановление названий функций объясненных_вариантов_расс_ в PCA с помощью sklearn
Я пытаюсь восстановиться после PCA, выполненного с помощью scikit-learn, какие функции выбраны как актуальные.
Классический пример с набором данных IRIS.
import pandas as pd
import pylab as pl
from sklearn import datasets
from sklearn.decomposition import PCA
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
df_norm = (df - df.mean()) / df.std()
# PCA
pca = PCA(n_components=2)
pca.fit_transform(df_norm.values)
print pca.explained_variance_ratio_
Это возвращает
In [42]: pca.explained_variance_ratio_
Out[42]: array([ 0.72770452, 0.23030523])
Как я могу восстановить, какие две особенности позволяют эти две объясненные различия среди набора данных? Сказал иначе, как я могу получить индекс этой функции в iris.feature_names?
In [47]: print iris.feature_names
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Заранее спасибо за помощь.
4 ответа
Эта информация включена в pca атрибут: components_, Как описано в документации, pca.components_ выводит массив [n_components, n_features], чтобы понять, как компоненты линейно связаны с различными функциями, вам необходимо:
Примечание: каждый коэффициент представляет корреляцию между определенной парой компонента и признака
import pandas as pd
import pylab as pl
from sklearn import datasets
from sklearn.decomposition import PCA
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
from sklearn import preprocessing
data_scaled = pd.DataFrame(preprocessing.scale(df),columns = df.columns)
# PCA
pca = PCA(n_components=2)
pca.fit_transform(data_scaled)
# Dump components relations with features:
print pd.DataFrame(pca.components_,columns=data_scaled.columns,index = ['PC-1','PC-2'])
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
PC-1 0.522372 -0.263355 0.581254 0.565611
PC-2 -0.372318 -0.925556 -0.021095 -0.065416
ВАЖНО: В качестве дополнительного комментария обратите внимание, что знак PCA не влияет на его интерпретацию, поскольку знак не влияет на дисперсию, содержащуюся в каждом компоненте. Важны только относительные признаки признаков, формирующих измерение PCA. Фактически, если вы снова запустите код PCA, вы можете получить размеры PCA с инвертированными знаками. Для интуитивного представления об этом подумайте о векторе и его негативе в трехмерном пространстве - оба по существу представляют одно и то же направление в пространстве. Проверьте этот пост для дальнейшего использования.
Изменить: как прокомментировали другие, вы можете получить те же значения из .components_ приписывать.
Каждый главный компонент представляет собой линейную комбинацию исходных переменных:
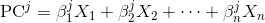
где X_i s - исходные переменные, и Beta_i s - соответствующие веса или так называемые коэффициенты.
Чтобы получить вес, вы можете просто передать идентификационную матрицу transform метод:
>>> i = np.identity(df.shape[1]) # identity matrix
>>> i
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
>>> coef = pca.transform(i)
>>> coef
array([[ 0.5224, -0.3723],
[-0.2634, -0.9256],
[ 0.5813, -0.0211],
[ 0.5656, -0.0654]])
Каждый столбец coef Матрица выше показывает веса в линейной комбинации, которая получает соответствующий главный компонент:
>>> pd.DataFrame(coef, columns=['PC-1', 'PC-2'], index=df.columns)
PC-1 PC-2
sepal length (cm) 0.522 -0.372
sepal width (cm) -0.263 -0.926
petal length (cm) 0.581 -0.021
petal width (cm) 0.566 -0.065
[4 rows x 2 columns]
Например, выше показано, что второй основной компонент (PC-2) в основном соответствует sepal width, который имеет самый высокий вес 0.926 в абсолютном выражении;
Поскольку данные были нормализованы, вы можете подтвердить, что основные компоненты имеют дисперсию 1.0 что эквивалентно каждому коэффициентному вектору, имеющему норму 1.0:
>>> np.linalg.norm(coef,axis=0)
array([ 1., 1.])
Можно также подтвердить, что главные компоненты могут быть рассчитаны как произведение точек вышеуказанных коэффициентов и исходных переменных:
>>> np.allclose(df_norm.values.dot(coef), pca.fit_transform(df_norm.values))
True
Обратите внимание, что нам нужно использовать numpy.allclose вместо обычного оператора равенства, из-за ошибки точности с плавающей точкой.
То, как сформулирован этот вопрос, напоминает мне о неправильном понимании принципа анализа компонентов, когда я впервые пытался понять его. Я хотел бы пройти через это здесь в надежде, что другие не будут тратить на дорогу в никуда столько времени, сколько я делал до того, как пенни наконец упала.
Понятие "восстановление" названий функций предполагает, что PCA идентифицирует те функции, которые наиболее важны в наборе данных. Это не совсем верно.
Как я понимаю, PCA идентифицирует объекты с наибольшим разбросом в наборе данных и затем может использовать это качество набора данных для создания меньшего набора данных с минимальной потерей описательной силы. Преимущества меньшего набора данных в том, что он требует меньше вычислительной мощности и должен иметь меньше шума в данных. Но особенности наибольшей дисперсии не являются "лучшими" или "наиболее важными" характеристиками набора данных, поскольку можно сказать, что такие концепции вообще существуют.
Чтобы воплотить эту теорию в практический пример приведенного выше примера кода @ Rafa:
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
from sklearn import preprocessing
data_scaled = pd.DataFrame(preprocessing.scale(df),columns = df.columns)
# PCA
pca = PCA(n_components=2)
pca.fit_transform(data_scaled)
учитывать следующее:
post_pca_array = pca.fit_transform(data_scaled)
print data_scaled.shape
(150, 4)
print post_pca_array.shape
(150, 2)
В этом случае, post_pca_array имеет те же 150 строк данных, что и data_scaled, но data_scaledЧетыре столбца были сокращены с четырех до двух.
Критическим моментом здесь является то, что два столбца - или компоненты, чтобы быть терминологически согласованными - post_pca_array не являются двумя "лучшими" столбцами data_scaled, Это две новые колонки, определяемые алгоритмом sklearn.decomposition"s PCA модуль. Второй столбец, PC-2 в примере @ Rafa, сообщает sepal_width больше, чем любой другой столбец, но значения в PC-2 а также data_scaled['sepal_width'] не то же самое.
Таким образом, хотя интересно узнать, какой вклад каждый столбец в исходных данных вносил в компоненты набора данных после PCA, понятие "восстановления" имен столбцов немного вводит в заблуждение и, безусловно, вводило меня в заблуждение в течение длительного времени. Единственная ситуация, когда между столбцами после PCA и исходными столбцами будет совпадение, будет иметь место, если число основных компонентов будет равно количеству столбцов в оригинале. Однако не было бы смысла использовать одинаковое количество столбцов, потому что данные не изменились бы. Вы бы только пошли туда, чтобы вернуться снова, как это было.
Важными характеристиками являются те, которые оказывают большее влияние на компоненты и, следовательно, имеют большое абсолютное значение / коэффициент / нагрузку на компонент.
Получить the most important feature name на ПК:
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np
np.random.seed(0)
# 10 samples with 5 features
train_features = np.random.rand(10,5)
model = PCA(n_components=2).fit(train_features)
X_pc = model.transform(train_features)
# number of components
n_pcs= model.components_.shape[0]
# get the index of the most important feature on EACH component i.e. largest absolute value
# using LIST COMPREHENSION HERE
most_important = [np.abs(model.components_[i]).argmax() for i in range(n_pcs)]
initial_feature_names = ['a','b','c','d','e']
# get the names
most_important_names = [initial_feature_names[most_important[i]] for i in range(n_pcs)]
# using LIST COMPREHENSION HERE AGAIN
dic = {'PC{}'.format(i+1): most_important_names[i] for i in range(n_pcs)}
# build the dataframe
df = pd.DataFrame(sorted(dic.items()))
Это печатает:
0 1
0 PC1 e
1 PC2 d
Заключение / Объяснение:
Так что на ПК1 функция под названием e является наиболее важным и на ПК2 d ,
Учитывая вашу установленную оценку pca, компоненты должны быть найдены в pca.components_, которые представляют направления наибольшей дисперсии в наборе данных.