Итеративная сложность времени возведения в квадрат
У меня есть следующая реализация повторного возведения в квадрат:
def power(a, b):
result = 1
while b > 0:
if b % 2 == 1:
result = mult(result, a)
a = mult(a, a)
b = b // 2
return result
mult() Метод умножает 2 заданных числа, если, если один имеет длину x биты, а другой имеет длину y бит, количество операций, которые умножение займет x*y+(x+y) операции, которые мне нужно учитывать при анализе сложности.
И я пытаюсь найти O() границу обозначения числа арифметических операций, выполняемых как функция n а также m когда длина a равна n битам, а длина b равна m битам. Мне нужно учитывать только умножение строк и проверять наихудший случай.
Худший случай, когда b м-битное число, где все m двоичные цифры 1, а затем у меня есть m итерации цикла, где на каждой итерации условие if выполняется.
Что я не знаю, как это сделать, так это то, как я должен учитывать в своих вычислениях тот факт, что a растет для каждой итерации? Как мне выразить это в некоторой конечной сумме с, вероятно, геометрической прогрессией, которую я могу вычислить?
Спасибо
3 ответа
Кроме того, я знаю, что умножение на 2 числа x битов и y битов приведет к арифметическим операциям x*y+(x+y).
Это не (в общем) правда. Процессор умножит два числа за определенное количество циклов, независимо от того, большие они или нет. Если вы не имеете дело с огромными числами, вы должны рассмотреть, относительно асимптотической сложности (O), умножение как одну операцию, и то же самое относится к сложению, делению,...
В вашем коде у вас есть три из четырех операций за итерацию цикла (if b % 2 == 1, может быть result = result*a, a = a*a, b = b // 2). Сложность зависит только от количества итераций цикла, то есть: log2(b), потому что b делится на два в каждой итерации.
Для больших чисел у вас есть две операции, которые могут повлиять на асимптотическую сложность: result = result*a а также a = a*a, Cpython использует умножение Карацубы, которое равно O(n^log2(3)), если n - это число цифр, если числа.
Я просто уточню a*a, Когда вы берете квадрат числа, вы примерно умножаете количество цифр на две. Рассмотрим циклы log2 (b): a*a возьмите O(n^log2(3)) в первой итерации, O(2n^log2(3)) во второй, O(4n^log2(3)) во вторую, ..., O(bn)^log2(3)) в последнем. Сумма O((b*log2(b)*n)^log2(3)), если я не ошибаюсь!
За a*aЕсли вы привязаны к алгоритму мутации O(x*y), то для ваших циклов log2 (b)
- O (n ^ 2) для первой итерации;
- O ((2n) ^ 2) для второй итерации;
- O ((4n) ^ 2) для третьей итерации;
- O ((2 ^ (k-1) * n) ^ 2) для k-й итерации.
Это O(b^2 * n^2) = O(2^2m * n^2) Я думаю (сейчас нет времени проверять!).
Я думаю, что сложность этого алгоритма не зависит от.
При рассмотрении сложности, я думаю, что число циклов является вашим основным показателем для наибольшей сложности из-за m.
Перебирая значения b, мы можем увидеть следующее число, если b > 0 вычислений как:
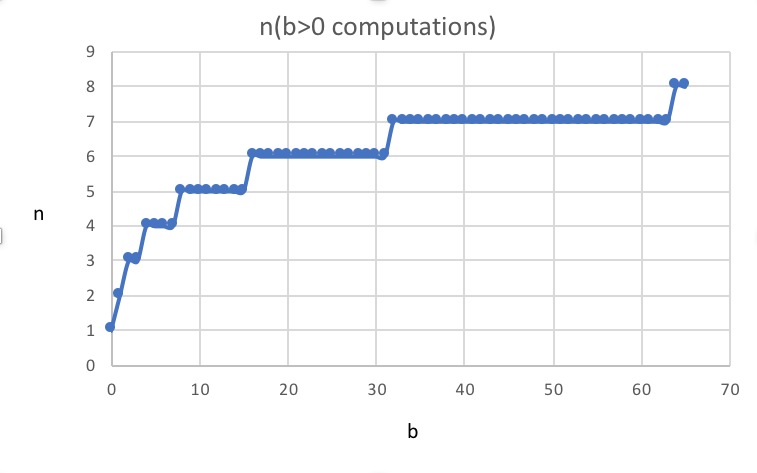 0) вычислений для значения b">
0) вычислений для значения b">
Интересно, что мы видим увеличение n циклов для каждого кратного 2 (т.е. 1,2,4,8,16,32,64).
Грубо говоря, я бы сказал, что сложность этого алгоритма тесно связана с O(log2(n)).
Ну, после некоторого анализа, я думаю, что число итераций power Метод будет суммой по i (от 0 до m-1) из: 2^(2i-1)*n+(2^(i-1)+2^i*n+(2^i*n)^2+2^(i+1)*n и это довольно просто, чтобы получить сложность: O(4^m*n^2)