Подходит ли команда MATLAB lsim для линеаризованных моделей пространства состояний?

Question

Модель пространства состояний имеет вид: dx = Ax + Bu y = Cx + Du

Нелинейные модели пространства состояний, которые линеаризуются, имеют вид:

dΔx = AΔx + BΔu
Δy =  CΔx + DΔu

Куда:

Δx = [x1 - x10; x2 - x20; x3 - x30; .... ; xn - xn0]
Δu = [u1 - u10; u2 - u20; u3 - u30; .... ; um - um0]

X10, x20, x30, xn0, u10, u20, u30, um0 - это постоянные / начальные значения для линеаризации.

Так! Вопрос о команде MATLAB "lsim":

lsim (sys, u, t, x0)

В этом случае sys - это матрицы A, B, C, D из модели пространства линейных состояний. u - вектор сигнала, t - вектор времени. Но х0.... могу ли я сказать, что х0 - это х10, х20, х30, ...., хн0?

Могу ли я также сказать, что u = u - u0, а u0 - это, u10, u10, u20, u30, ..., um0?

Пример:

u = linspace(5, 5, 100); % insignal 5
t = linspace(0, 100, 100); % 100 seconds
u0 = [0.2; -1.2; -3];
u = u - u0; % 
x0 = [-2; 2; -1]
lsim (sys, u, t, x0)

Это приведет к результатам:

Δx = [x1 - 2; x2 + 2; x3 - 1]
Δu = [u1 + 0.2; u2 - 1.2; u3 - 3]

Я прав?

Answer 1

Существует легкодоступная Simulink S-функция dsfunc.m которая представляет собой имитацию модели пространства состояний и которая может быть легко адаптирована для включенных линеаризованных матриц пространства состояний, изменяющихся на каждом временном шаге.

Просто создайте файл simulink dsfunc.slx и запустите его с помощью команды sim sim('dsfunc') команда.

Хорошей частью является то, что S-функция правильно работает с состоянием, и вы просто каждый раз адаптируете модель пространства состояний, сохраняя состояние от одной итерации к другой.

Также вы можете сделать это одинаково легко с одним for петля. Константа линеаризации включены, как показано.

function [t,u,x,y]=example2
% Start
dt=0.001;
N=1000;
n=2;
r=1;
t=(0:N-1)'*dt;
u=rand(N,r);
% First
[A,B,C,D,x0,y0]=ABCD(t(1),zeros(n,1),u(1,:)');
x(1,:)=x0';
y(1,:)=(C*x(1,:)'+D*u(1,:)'+y0)';
% Cycle
for i=2:N
    [A,B,C,D,x0,y0]=ABCD(t(i),x(i-1,:)',u(i-1,:)');
    x(i,:)=(A*x(i-1,:)'+B*u(i-1,:)'+x0)';
    y(i,:)=(C*x(i,:)'+D*u(i,:)'+y0)';
end
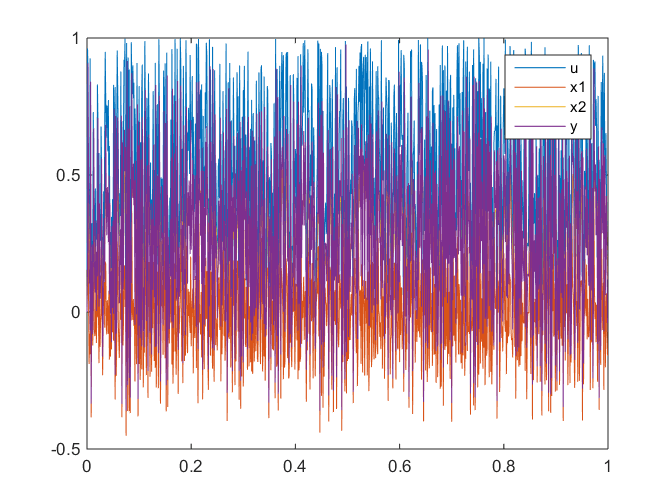
plot(t,[u x y]);legend({'u' 'x1' 'x2' 'y'});


function [A,B,C,D,x0,y0]=ABCD(t,x,u)
A=[0.1 -0.9;0 0.1];
B=0.5*ones(2,1);
C=[1 1];
x0=[0];y0=[0];