Как генерировать равноразмерные интерполяционные значения

Question

У меня есть список (x,y) значений, которые не распределены равномерно. Вот архив, используемый в этом вопросе.

Я могу интерполировать между значениями, но то, что я получаю, не равнораспределенные точки интерполяции. Вот что я делаю:

x_data = [0.613,0.615,0.615,...]
y_data = [5.919,5.349,5.413,...]

# Interpolate values for x and y.
t = np.linspace(0, 1, len(x_data))
t2 = np.linspace(0, 1, 100)
# One-dimensional linear interpolation.
x2 = np.interp(t2, t, x_data)
y2 = np.interp(t2, t, y_data)

# Plot x,y data.
plt.scatter(x_data, y_data, marker='o', color='k', s=40, lw=0.)

# Plot interpolated points.
plt.scatter(x2, y2, marker='o', color='r', s=10, lw=0.5)

Что приводит к:

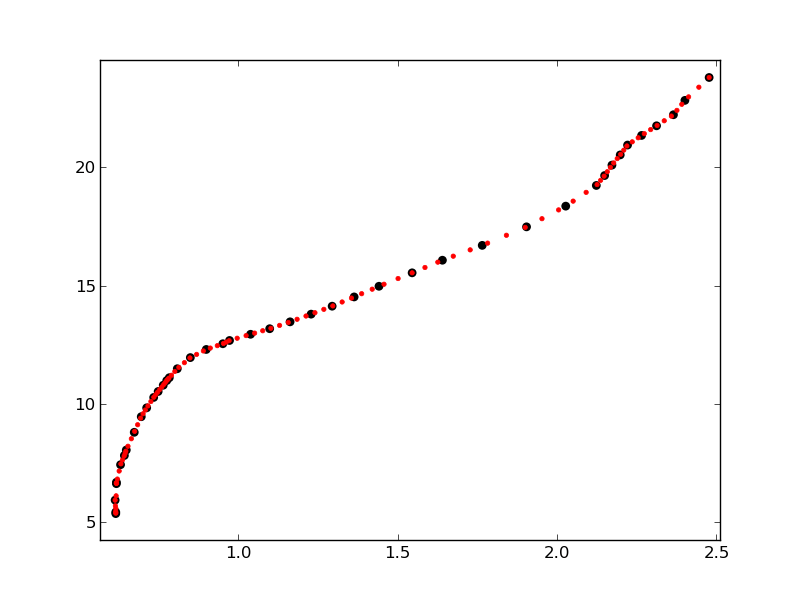
Как можно видеть, красные точки расположены ближе друг к другу на участках графика, где исходное распределение точек более плотное.

Мне нужен способ для генерации интерполированных точек, равных по x, y в соответствии с заданным значением шага (скажем, 0,1)

---

Как правильно указывает askewchan, когда я имею в виду " равнозначно по x, y", я имею в виду, что две последовательные интерполированные точки на кривой должны быть удалены друг от друга (евклидово расстояние по прямой линии) на одно и то же значение.

---

Я попробовал ответ unubtu, и он хорошо работает для гладких кривых, но, кажется, ломается для не очень гладких:

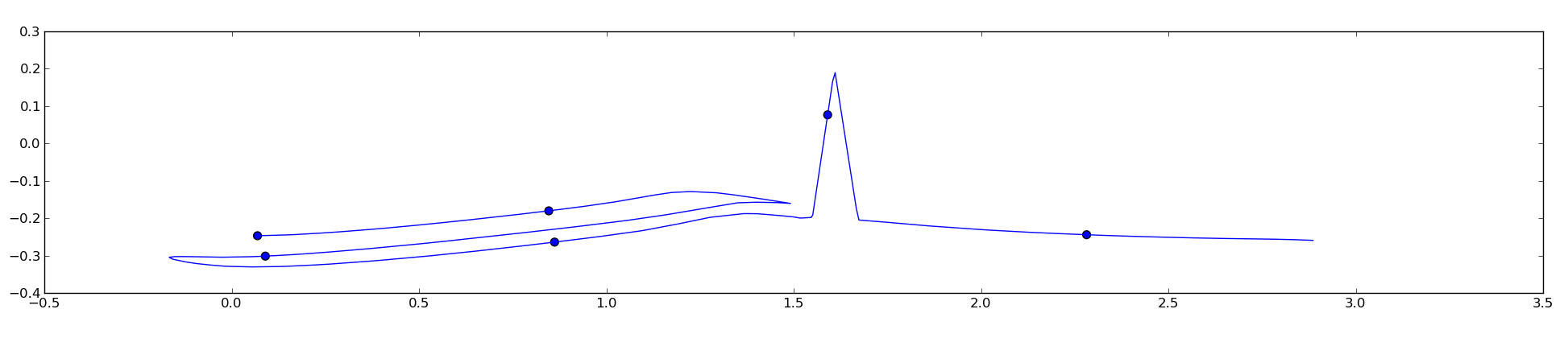
Это происходит потому, что код вычисляет евклидово расстояние до точки, а не непосредственно по кривой, и мне нужно, чтобы расстояние по кривой было одинаковым между точками. Можно ли как-то обойти эту проблему?

Answer 1

Давайте сначала рассмотрим простой случай. Предположим, ваши данные выглядят как синяя линия ниже.

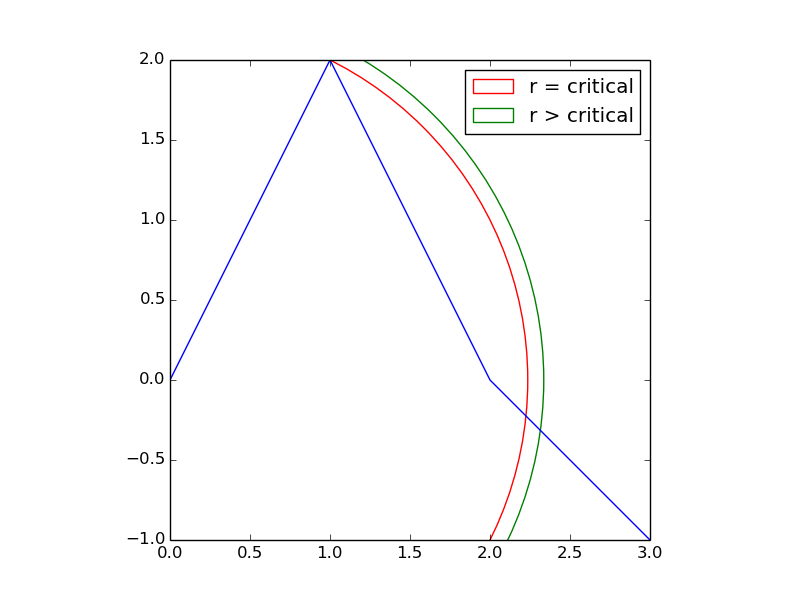
Если вы хотите выбрать равноудаленные точки, которые были r расстояние друг от друга, тогда будет какое-то критическое значение для r где острие в (1,2) является первой равноудаленной точкой.

Если вы хотите, чтобы точки были больше, чем это критическое расстояние друг от друга, то первая равноудаленная точка перепрыгнула бы из (1,2) в какое-то совсем другое место - изображенное пересечением зеленой дуги с синей линией. Изменение не является постепенным.

Этот игрушечный чехол говорит о небольшом изменении параметра r может оказать радикальное, прерывистое влияние на решение.

Это также предполагает, что вы должны знать местоположение i-й равноудаленной точки, прежде чем сможете определить местоположение (i+1)-ой равноотстоящей точки.

Похоже, требуется итеративное решение:

import numpy as np
import matplotlib.pyplot as plt
import math

x, y = np.genfromtxt('data', unpack=True, skip_header=1)
# find lots of points on the piecewise linear curve defined by x and y
M = 1000
t = np.linspace(0, len(x), M)
x = np.interp(t, np.arange(len(x)), x)
y = np.interp(t, np.arange(len(y)), y)
tol = 1.5
i, idx = 0, [0]
while i < len(x):
    total_dist = 0
    for j in range(i+1, len(x)):
        total_dist += math.sqrt((x[j]-x[j-1])**2 + (y[j]-y[j-1])**2)
        if total_dist > tol:
            idx.append(j)
            break
    i = j+1

xn = x[idx]
yn = y[idx]
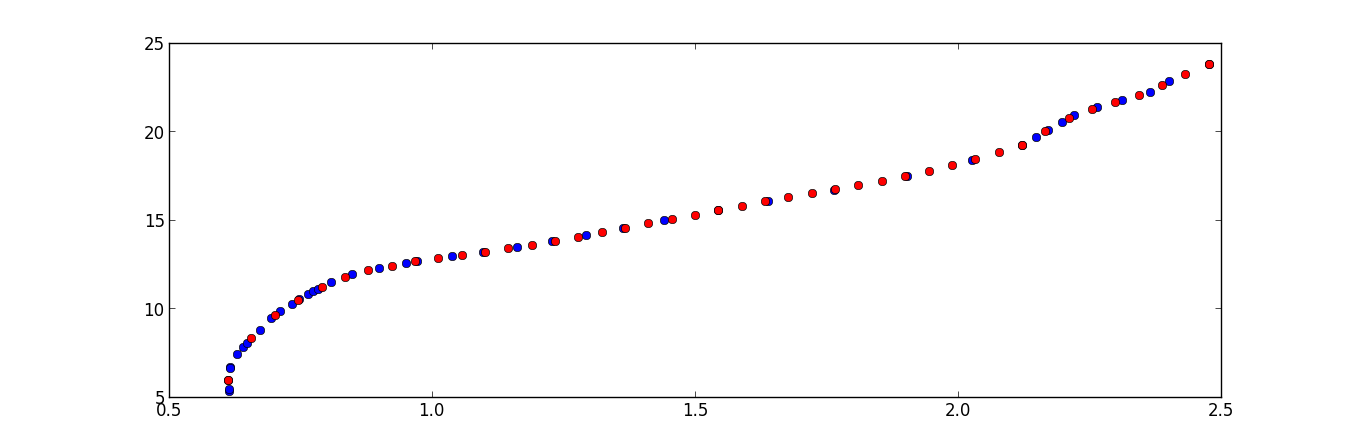
fig, ax = plt.subplots()
ax.plot(x, y, '-')
ax.scatter(xn, yn, s=50)
ax.set_aspect('equal')
plt.show()

Примечание: я установил соотношение сторон на 'equal' чтобы было более очевидно, что точки равноудалены.

Answer 2

Преобразуйте ваши данные xy в параметризованную кривую, то есть вычислите все расстояния между точками и сгенерируйте координаты на кривой с помощью кумулятивного суммирования. Затем интерполируйте x- и y-координаты независимо относительно новых координат.

import numpy as np
from pylab import plot

data = '''    0.613   5.919
    0.615   5.349
    0.615   5.413
    0.617   6.674
    0.617   6.616
    0.63    7.418
    0.642   7.809
    0.648   8.04
    0.673   8.789
    0.695   9.45
    0.712   9.825
    0.734   10.265
    0.748   10.516
    0.764   10.782
    0.775   10.979
    0.783   11.1
    0.808   11.479
    0.849   11.951
    0.899   12.295
    0.951   12.537
    0.972   12.675
    1.038   12.937
    1.098   13.173
    1.162   13.464
    1.228   13.789
    1.294   14.126
    1.363   14.518
    1.441   14.969
    1.545   15.538
    1.64    16.071
    1.765   16.7
    1.904   17.484
    2.027   18.36
    2.123   19.235
    2.149   19.655
    2.172   20.096
    2.198   20.528
    2.221   20.945
    2.265   21.352
    2.312   21.76
    2.365   22.228
    2.401   22.836
    2.477   23.804'''

data = np.array([line.split() for line in data.split('\n')],dtype=float)

x,y = data.T
xd =np.diff(x)
yd = np.diff(y)
dist = np.sqrt(xd**2+yd**2)
u = np.cumsum(dist)
u = np.hstack([[0],u])

t = np.linspace(0,u.max(),20)
xn = np.interp(t, u, x)
yn = np.interp(t, u, y)

plot(x,y,'o')
plot(xn,yn,'gs')
xlim(0,5.5)
ylim(10,17.5)

Answer 3

Расширяя ответ @Christian K., вот как это сделать для многомерных данных с помощью scipy.interpolate.interpn. Допустим, мы хотим выполнить повторную выборку до 10 равноотстоящих точек:

import numpy as np
import scipy
# Assuming that 'data' is rows x dims (where dims is the dimensionality)
diffs = data[1:, :] - data[:-1, :]
dist = np.linalg.norm(diffs, axis=1)
u = np.cumsum(dist)
u = np.hstack([[0], u])
t = np.linspace(0, u[-1], 10)
resampled = scipy.interpolate.interpn((u,), pts, t)

Answer 4

Следующий скрипт будет интерполировать точки с равным шагом x_max - x_min / len(x) = 0.04438

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt

data = np.loadtxt('data.txt')
x = data[:,0]
y = data[:,1]

f = interp1d(x, y)
x_new = np.linspace(np.min(x), np.max(x), x.shape[0])
y_new = f(x_new)

plt.plot(x,y,'o', x_new, y_new, '*r')
plt.show()

Answer 5

Возможно создать эквидистантные точки вдоль кривой. Но должно быть больше определения того, что вы хотите для реального ответа. Извините, но код, который я написал для этой задачи, находится в MATLAB, но я могу описать общие идеи. Есть три варианта.

Во-первых, должны ли точки быть действительно равноудаленными от соседей с точки зрения простого евклидова расстояния? Для этого потребуется найти пересечение в любой точке кривой с окружностью фиксированного радиуса. Тогда просто шагай по кривой.

Далее, если вы намерены определить расстояние, чтобы обозначить расстояние вдоль самой кривой, если кривая является кусочно-линейной, то проблему снова легко решить. Просто сделайте шаг по кривой, так как расстояние на отрезке линии легко измерить.

Наконец, если вы хотите, чтобы кривая была кубическим сплайном, опять же, это не невероятно сложно, но это немного больше работы. Здесь хитрость заключается в следующем:

• Вычислить кусочно-линейную длину дуги от точки к точке вдоль кривой. Назовите это т.
• Создайте пару кубических сплайнов, x(t), y(t).
• Дифференцируйте x и y как функции от t. Поскольку это кубические сегменты, это легко. Производные функции будут кусочно-квадратичными.
• Используйте решатель оды для перемещения по кривой, интегрируя дифференциальную функцию длины дуги. В MATLAB ODE45 работал хорошо.

Таким образом, один интегрирует

sqrt((x')^2 + (y')^2)

Опять же, в MATLAB ODE45 можно установить для определения тех мест, где функция пересекает определенные заданные точки.

Если ваши навыки работы с MATLAB соответствуют поставленной задаче, вы можете посмотреть код в interparc для более подробного объяснения. Это достаточно хорошо прокомментированный код.