Как рассчитать эту логарифмическую сложность с помощью суммирования?

Question

Мой вопрос

Какова сложность Big-O для этого фрагмента кода? Рассмотрим n как степень 4.

for(int i = 1; i <= n; i = i*4)                      
    for(int k = 1; k <= i; k++)                 
       // constant statement

Что я знаю до сих пор

Я попытался превратить этот код в суммирование, чтобы найти сложность. Вот что я получил: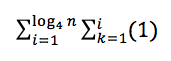

Я получил (база 4) log(n), вычисляя ряды 4, 4^2, 4^3 ... 4^r = n. r = (основание 4) log(n).

Я сейчас застрял в этом суммировании:

Пожалуйста, дайте мне знать, если я делаю что-то не так или есть другой способ сделать это.

Answer 1

Вы на правильном пути, но ваше внутреннее суммирование неверно. Вы правы, что внешний цикл будет повторять log_4 n раз, но вы настроили внешнюю сумму так, чтобы я считал 1, 2, 3, ..., log_4 n, а не 4^0, 4^1, 4^2, ... 4^log_4 n. В результате верхняя граница этого внутреннего суммирования неверна. Граница должна быть 4 ^ я, а не я.

Если вы все настроите таким образом, вы обнаружите, что общая сумма

4 ^ 0 + 4 ^ 1 + 4 ^ 2 +... + 4 ^ log_4 n

= (4 ^ (log_4 n + 1) - 1) / (4 - 1) (используя формулу для суммы геометрического ряда

= (4 (4 ^ log_4 n) - 1) / 3

= (4n - 1) / 3

= Θ (n).

Answer 2

Вы можете использовать wolframalpha, чтобы получить результат с чрезвычайной точностью.

https://www.wolframalpha.com/input/?i=sum+i,+i%3D1+to+log_4(n)