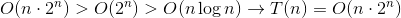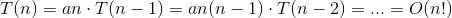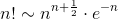Какой из следующего кода имеет меньшую временную сложность? Объясните пожалуйста как рассчитать

Question

Ниже приведен код для расчета подмножеств данного массива:

1. Метод битовой манипуляции: как его анализировать?

    vector<vector<int>> subsets(vector<int>& nums)
     {
        sort(nums.begin(), nums.end());
   
        int num_subset = pow(2, nums.size()); 
        vector<vector<int> > res(num_subset, vector<int>());
   
        for (int i = 0; i < nums.size(); i++)
            for (int j = 0; j < num_subset; j++)
                if ((j >> i) & 1)
                    res[j].push_back(nums[i]);
   
        return res;  
     }
   

2. Метод отслеживания: как это проанализировать

        vector<vector<int>> subsets(vector<int>& nums)
         {
           sort(nums.begin(), nums.end()); // sort the original array
           vector<vector<int>> subs;
           vector<int> sub;  
           genSubsets(nums, 0, sub, subs);
           return subs; 
         }
   
       void genSubsets(vector<int>& nums, int start, vector<int>& sub,vector<vector<int>>& subs)
         {
           subs.push_back(sub);
           for (int i = start; i < nums.size(); i++) {
            sub.push_back(nums[i]);
            genSubsets(nums, i + 1, sub, subs);
            sub.pop_back();
          }
        }
   

Answer 1

Векторные операции: - push_back а также pop_back оба O(1)- конструктор с аргументом размера n является O(n)

---

Метод манипуляции битами:

• sort является O(n log n)
• Возведение res является O(nums_subset) = O(2^n)

• Внешний цикл выполнен n раз, внутренний nums_subset = 2^n раз.

  

---

Метод возврата:

• Снова, sort является O(n log n)

• каждый genSubsets цикл вызовов через nums.size() - start раз, каждый раз выполняя рекурсивный вызов с циклом на 1 меньше.

  

---

Какой больше? По приближению Стерлинга,

Так что возвращение назад обходится дороже.