Определение "DFA для языка"
Я только начал изучать теорию вычислений в этом семестре и немного смутился из-за фразы "DFA для языка". Если его попросили построить DFA для некоторого набора двоичных строк L, значит ли это найти DFA M с L(M)=L или просто $L(M)\supset L$?
3 ответа
Большинство курсов по компилятору / теории имеют разные стили, связанные с обучающими определениями детерминированных конечных автоматов и формальных языков, но я постараюсь сделать это описание как можно более независимым.
Фраза "DFA для языка" в широком смысле означает: DFA, который принимает каждый word на языке и отвергает каждый word не на языке. То, как меня учили DFA, состоит в том, чтобы иметь конечные / принимающие состояния и регулярные состояния, что устраняет необходимость в неявном состоянии ошибки. Это означает, что DFA принимает слово, если в конце ввода находится состояние, в котором он находится accepting и он отклоняет слово, если государство не accepting,
Пример:
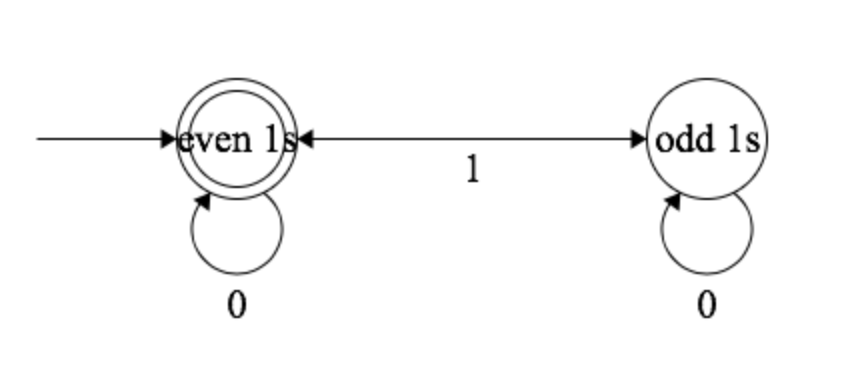
Давайте определим L как язык, который содержит четное число 1. Это будут двоичные строки, поэтому символы будут только 0 и 1. 00, 110, 111, 1111 и т. д. являются примерами слов на этом языке. Обратите внимание, что пустая строка на этом языке.
У нас может быть два государства в нашем DFA. Начальное состояние, давайте назовем это even 1s, также является принимающим состоянием, потому что 0 из них является четным. Другое состояние odd 1s Это не принимает.
Что касается переходов, когда even 1s получает 1, он переходит к odd 1s, И когда odd 1s получает 1, он переходит к even 1s, Теперь число 0 не имеет значения, поэтому в любом из состояний оно переходит в себя.
Извиняюсь за двойную стрелку, этот сайт отличный, но я не мог понять, как разделить переходы между even 1s а также odd 1s
Детерминированный конечный автомат (DFA) В DFA для каждого входного символа можно определить состояние, в которое перейдет автомат. Следовательно, он называется детерминированным автоматом. Поскольку число состояний конечно, машина называется детерминированной конечной машиной или детерминированным конечным автоматом.
Формальное определение ДКА ДКА может быть представлен набором из 5 (Q, ∑, δ, q0, F), где —
-> Q — конечное множество состояний.
-> ∑ — это конечное множество символов, называемое алфавитом.
-> δ — функция перехода, где δ: Q × ∑ → Q
-> q0 — начальное состояние, из которого обрабатывается любой ввод (q0 ∈ Q).
-> F — множество конечных состояний/состояний Q (F ⊆ Q).
Напишите свой вопрос точно. здесь DFA для языка означает, что вам нужно создать машину только для конкретного языка, а не для его подмножества или надмножества. построить DFA maachine, для которого L(M)= L.