Как применить двоичную маску и STFT для создания аудиофайла?

Question

Как применить двоичную маску и STFT для создания аудиофайла?

Итак, вот идея: вы можете сгенерировать спектрограмму из аудиофайла, используя кратковременное преобразование Фурье (stft). Затем некоторые люди сгенерировали нечто, называемое "двоичной маской", чтобы сгенерировать другой звук (т. Е. С удаленным фоновым шумом и т. Д.) Из обратного кадра.

Вот что я понимаю:

Stft представляет собой простое уравнение, которое применяется к аудиофайлу, который генерирует информацию, которая может легко отображать спектрограмму. Взяв обратную матрицу stft и умножив ее на матрицу одинакового размера (двоичную матрицу), вы можете создать новую матрицу с информацией для создания аудиофайла с замаскированным звуком.

Как только я делаю матричное умножение, как создается новый аудиофайл?

Это немного, но вот что у меня есть с точки зрения кода:

from librosa import load
from librosa.core import stft, istft
y, sample_rate = load('1.wav')
spectrum = stft(y)
back_y = istft(spectrum)

Спасибо, и вот несколько слайдов, которые дали мне это далеко. Я был бы признателен, если бы вы могли дать мне пример / демо в Python

0

python audio linear-algebra librosa spectrogram

Источник

user5038566 02 авг '18 в 13:38

1 ответ

Другие вопросы по тегам python audio linear-algebra librosa spectrogram

user500207 09 авг '18 в 18:11 2018-08-09 18:11 · Answer 1 · 2018-08-09 18:11

STFT Librosa является полнофункциональным, поэтому, если вы не будете очень осторожны с манипулированием спектром, вы не получите ощутимого результата от его istft,

Вот пара функций, stft а также istft, который я написал с нуля, который представляет прямой и обратный STFT, наряду с вспомогательным методом, который дает вам временные и частотные местоположения каждого пикселя в массиве STFT, плюс демонстрацию:

import numpy as np
import numpy.fft as fft


def stft(x, Nwin, Nfft=None):
    """
    Short-time Fourier transform: convert a 1D vector to a 2D array

    The short-time Fourier transform (STFT) breaks a long vector into disjoint
    chunks (no overlap) and runs an FFT (Fast Fourier Transform) on each chunk.

    The resulting 2D array can 

    Parameters
    ----------
    x : array_like
        Input signal (expected to be real)
    Nwin : int
        Length of each window (chunk of the signal). Should be ≪ `len(x)`.
    Nfft : int, optional
        Zero-pad each chunk to this length before FFT. Should be ≥ `Nwin`,
        (usually with small prime factors, for fastest FFT). Default: `Nwin`.

    Returns
    -------
    out : complex ndarray
        `len(x) // Nwin` by `Nfft` complex array representing the STFT of `x`.

    See also
    --------
    istft : inverse function (convert a STFT array back to a data vector)
    stftbins : time and frequency bins corresponding to `out`
    """
    Nfft = Nfft or Nwin
    Nwindows = x.size // Nwin
    # reshape into array `Nwin` wide, and as tall as possible. This is
    # optimized for C-order (row-major) layouts.
    arr = np.reshape(x[:Nwindows * Nwin], (-1, Nwin))
    stft = fft.rfft(arr, Nfft)
    return stft


def stftbins(x, Nwin, Nfft=None, d=1.0):
    """
    Time and frequency bins corresponding to short-time Fourier transform.

    Call this with the same arguments as `stft`, plus one extra argument: `d`
    sample spacing, to get the time and frequency axes that the output of
    `stft` correspond to.

    Parameters
    ----------
    x : array_like
        same as `stft`
    Nwin : int
        same as `stft`
    Nfft : int, optional
        same as `stft`
    d : float, optional
        Sample spacing of `x` (or 1 / sample frequency), units of seconds.
        Default: 1.0.

    Returns
    -------
    t : ndarray
        Array of length `len(x) // Nwin`, in units of seconds, corresponding to
        the first dimension (height) of the output of `stft`.
    f : ndarray
        Array of length `Nfft`, in units of Hertz, corresponding to the second
        dimension (width) of the output of `stft`.
    """
    Nfft = Nfft or Nwin
    Nwindows = x.size // Nwin
    t = np.arange(Nwindows) * (Nwin * d)
    f = fft.rfftfreq(Nfft, d)
    return t, f


def istft(stftArr, Nwin):
    """
    Inverse short-time Fourier transform (ISTFT)

    Given an array representing the output of `stft`, convert it back to the
    original samples.

    Parameters
    ----------
    stftArr : ndarray
        Output of `stft` (or something the same size)
    Nwin : int
        Same input as `stft`: length of each chunk that the STFT was calculated
        over.

    Returns
    -------
    y : ndarray
        Data samples corresponding to STFT data.

    See also:
    stft : the forward transform
    """
    arr = fft.irfft(stftArr)[:, :Nwin]
    return np.reshape(arr, -1)


if __name__ == '__main__':
    sampleRate = 100.0  # Hertz
    N = 1024
    Nwin = 64

    # Generate a chirp: start frequency at 5 Hz and going down at 2 Hz/s
    time = np.arange(N) / sampleRate  # seconds
    x = np.cos(2 * np.pi * time * (5 - 2 * 0.5 * time))

    # Test with Nfft bigger than Nwin
    Nfft = Nwin * 2
    s = stft(x, Nwin, Nfft=Nfft)
    y = istft(s, Nwin)

    # Make sure the stft and istft are inverses. Caveat: `x` and `y` won't be
    # the same length if `N/Nwin` isn't integral!
    maxerr = np.max(np.abs(x - y))
    assert (maxerr < np.spacing(1) * 10)

    # Test `stftbins`
    t, f = stftbins(x, Nwin, Nfft=Nfft, d=1 / sampleRate)
    assert (len(t) == s.shape[0])
    assert (len(f) == s.shape[1])

    try:
        import pylab as plt
        plt.imshow(np.abs(s), aspect="auto", extent=[f[0], f[-1], t[-1], t[0]])
        plt.xlabel('frequency (Hertz)')
        plt.ylabel('time (seconds (start of chunk))')
        plt.title('STFT with chirp example')
        plt.show()
    except ModuleNotFoundError:
        pass

Это в самом деле, если вам легче читать.

Весь модуль принимает только реальные данные и использует Numpy's rfft функции. Вы можете определенно обобщить это для сложных данных (или использовать librosa), но для вашего приложения (маскирование звука) использование преобразований только для реальных данных позволяет легче убедиться, что все работает, и вывод обратного STFT является только действительным (это легко испортить, если вы делаете полностью общий сложный STFT, где вы должны быть осторожны в поддержании симметрии).

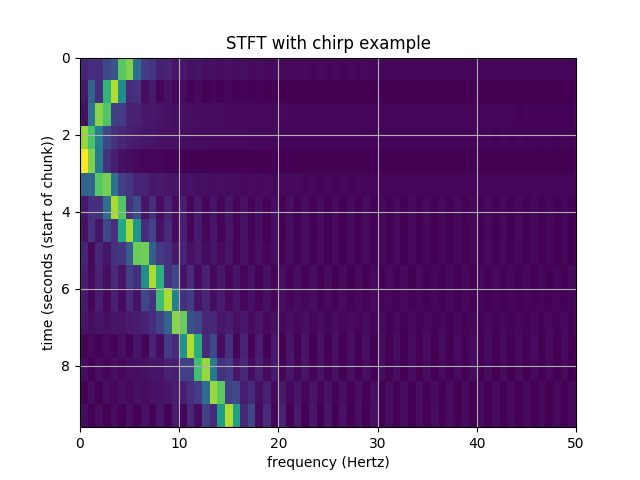
Демо сначала генерирует некоторые тестовые данные и подтверждает, что istft на stft данных производит данные снова. Тестовые данные - это ЛЧМ, который начинается с частоты 5 Гц и снижается с частотой 2 Гц в секунду, поэтому в течение ~10 секунд данных частота ЧИПа изменяется и заканчивается примерно на 15 Гц. Демонстрация строит график STFT (принимая абсолютное значение массива STFT):

Так

положить этот код в stft.py файл,
импортировать как import stft,
вычислить STFT как spectrum = stft.stft(y, 128),
визуализируйте свой спектр, как показано в демоверсии (не забудьте предварительно stft. к функциям, определенным в stft.py!),
выберите частоты, которые вы хотите ослабить / усилить и применить эти эффекты на spectrum массив, до
наконец получить обработанный звук через back_y = stft.istft(spectrum, 128),

Маскирование / усиление / ослабление частотного содержимого означает просто масштабирование некоторых элементов spectrum массив. Если у вас есть конкретные вопросы о том, как это сделать, сообщите нам об этом. Но, надеюсь, это даст вам надежный способ применения произвольных эффектов.

Если вы действительно хотите использовать функции librosa, дайте нам знать, и мы также сможем показать вам, как это сделать.