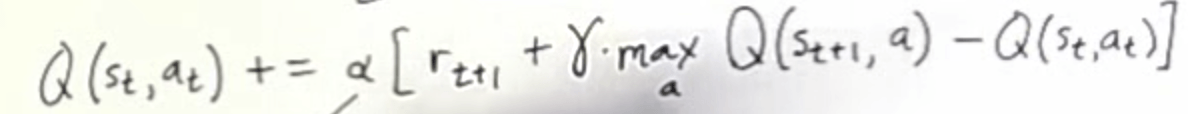Двойной учет в обучении с разницей во времени

Question

Я работаю над примером изучения временной разницы ( https://www.youtube.com/watch?v=XrxgdpduWOU), и у меня возникли некоторые проблемы со следующим уравнением в моей реализации на python, так как мне кажется, что я получаю двойное вознаграждение и Q.

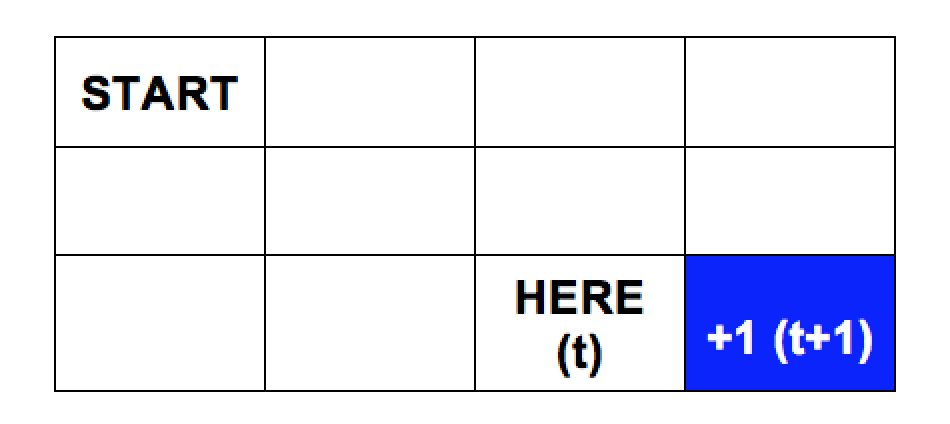
Если я закодирую приведенную ниже сетку в виде двумерного массива, мое текущее местоположение - (2, 2), а цель - (2, 3), предполагая, что максимальное вознаграждение равно 1. Пусть Q(t) - среднее значение моего текущего местоположения, тогда r(t+1) равно 1, и я предполагаю, что max Q(t+1) также равно 1, что приводит к тому, что мой Q(t) становится близким к 2 (предполагая, что гамма равна 1). Это правильно, или я должен предположить, что Q(n), где n является конечной точкой 0?

Отредактировано, чтобы включить код - я изменил функцию get_max_q так, чтобы она возвращала 0, если это конечная точка, и все значения теперь ниже 1 (что, я полагаю, является более правильным, поскольку вознаграждение составляет всего 1), но не уверен, что это правильный подход (ранее я установил, чтобы он возвращал 1, когда это была конечная точка).

#not sure if this is correct
def get_max_q(q, pos):
    #end point 
    #not sure if I should set this to 0 or 1
    if pos == (MAX_ROWS - 1, MAX_COLS - 1):
        return 0
    return max([q[pos, am] for am in available_moves(pos)])

def learn(q, old_pos, action, reward):
    new_pos = get_new_pos(old_pos, action)
    max_q_next_move = get_max_q(q, new_pos) 

    q[(old_pos, action)] = q[old_pos, action] +  alpha * (reward + max_q_next_move - q[old_pos, action]) -0.04

def move(q, curr_pos):
    moves = available_moves(curr_pos)
    if random.random() < epsilon:
        action = random.choice(moves)
    else:
        index = np.argmax([q[m] for m in moves])
        action = moves[index]

    new_pos = get_new_pos(curr_pos, action)

    #end point
    if new_pos == (MAX_ROWS - 1, MAX_COLS - 1):
        reward = 1
    else:
        reward = 0

    learn(q, curr_pos, action, reward)
    return get_new_pos(curr_pos, action)

=======================
OUTPUT
Average value (after I set Q(end point) to 0)
defaultdict(float,
            {((0, 0), 'DOWN'): 0.5999999999999996,
             ((0, 0), 'RIGHT'): 0.5999999999999996,
              ...
             ((2, 2), 'UP'): 0.7599999999999998})

Average value (after I set Q(end point) to 1)
defaultdict(float,
        {((0, 0), 'DOWN'): 1.5999999999999996,
         ((0, 0), 'RIGHT'): 1.5999999999999996,
         ....
         ((2, 2), 'LEFT'): 1.7599999999999998,
         ((2, 2), 'RIGHT'): 1.92,
         ((2, 2), 'UP'): 1.7599999999999998})

Answer 1

Значение Q представляет собой оценку того, какое вознаграждение вы ожидаете получить до конца эпизода. Итак, в состоянии терминала maxQ = 0, потому что вы не получите больше вознаграждений после этого. Таким образом, значение Q в t будет 1, что подходит для вашей недисконтированной проблемы. Но вы не можете игнорировать gamma в уравнении, добавьте его в формулу, чтобы сделать его со скидкой. Так, например, если gamma = 0.9значение Q при t будет 0,9. На (2,1) и (1,2) это будет 0,81 и так далее.