Подгонка сегмента в двухмерной плоскости

У меня проблемы со следующей проблемой

Учитывая, что N x S сетка и m сегментов параллельны горизонтальной оси (все они являются кортежами (x ', x' ', y)), ответьте на Q онлайн запросов формы (x', x ''). Ответ на такой запрос - наименьший у (если он есть) такой, что мы можем разместить сегмент (х ', х' ', у). Все сегменты не перекрываются, но начало одного сегмента может быть концом другого, то есть сегменты (x ', x' ', y) и (x' ', x' '', y) разрешены. Возможность разместить сегмент означает, что может существовать сегмент (x ', x' ', y), который не будет нарушать установленные правила, сегмент фактически не размещается (доска с начальными сегментами не изменяется), но мы только заявляем может быть один.

Ограничения

1 ≤ Q, S, m ≤ 10^5
1 ≤ N ≤ 10^9

Time: 1s
Memory: 256 Mb

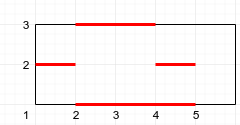
Вот пример по ссылке ниже. Входными сегментами являются (2, 5, 1), (1, 2, 2), (4, 5, 2), (2, 3, 3), (3, 4, 3).
Ответ на вопросы

1) (1, 2) → 1

2) (2, 3) → 2

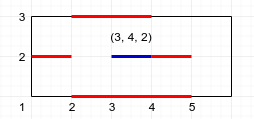
3) (3, 4) → 2

4) (4, 5) → 3

5) (1, 3) → невозможно разместить сегмент

Визуализированный ответ на третий запрос (синий сегмент):

Визуализированный ответ на третий запрос

Я не совсем понимаю, как подойти к проблеме. Это должно быть решено с помощью постоянного дерева сегментов, но я все еще не могу что-то придумать.

Не могли бы вы мне помочь, пожалуйста.

Это не моя домашняя работа. С источником проблемы можно ознакомиться здесь http://informatics.mccme.ru/mod/statements/view3.php?chapterid=111614. Английская версия оператора не доступна, и тестовый пример представляет входные данные по-другому, так что не обращайте внимания на исходные данные.

Источник

2 ответа

Решение

Вот решение времени O(N log N).

Предварительные сведения (хороший учебник доступен здесь): дерево сегментов, постоянное дерево сегментов.

Часть 0. Оригинальная постановка задачи

Я кратко опишу исходную формулировку проблемы, поскольку позже я буду говорить в ее терминах, а не в терминах абстрактных сегментов.

Есть поезд с S местами (S <= 10^5). Известно, что место s_i занято от времени l_i до времени r_i (не более 10 ^ 5 таких ограничений или пассажиров). Затем мы должны ответить на 10 ^ 5 запросов вида "найти наименьшее число мест, где время свободно от времени l_i до времени r_i, или сказать, что его нет". На все запросы нужно отвечать в режиме онлайн, то есть вы должны ответить на предыдущий запрос, прежде чем увидеть следующий.

Во всем тексте я обозначаю буквой N как количество мест, количество пассажиров и количество запросов, предполагая, что они имеют одинаковый порядок величины. Вы можете сделать более точный анализ, если это необходимо.

Часть 1. Ответ на один запрос

Давайте ответим на вопрос [L, R], предполагая, что после времени R. нет занятых мест. Для каждого места мы сохраняем последний раз, когда оно занято. Назовите это последним (S). Теперь ответом на запрос является минимум S, такой что last (S) <= L. Если мы построим дерево сегментов на местах, то мы сможем ответить на этот запрос за O(log ^ 2 N) времени: двоичный поиск значение S, проверьте, не превышает ли минимум диапазона на сегменте [0, S] L.

Тем не менее, этого может быть недостаточно, чтобы получить согласие. Нам нужен O(log N). Напомним, что каждый узел дерева сегментов хранит минимум в соответствующем диапазоне. Начнем с корня. Если минимум> = L, то для такого запроса нет места. В противном случае либо минимальное значение для левого или правого ребенка составляет <= L (или для обоих). В первом случае мы спускаемся к левому ребенку, во втором - вправо и повторяем, пока не достигнем листа. Этот лист будет соответствовать минимальному месту с последним (S) <= L.

Часть 2. Решение проблемы

Мы сохраняем постоянное дерево на местах, сохраняя последние (S) для каждого места (так же, как в предыдущей части). Давайте обработаем начальных пассажиров по порядку, отсортированных по их левой конечной точке в порядке возрастания. Для пассажира (s_i, l_i, r_i) мы обновляем дерево сегментов в позиции s_i значением r_i. Дерево является постоянным, поэтому мы храним новую копию где-то.

Чтобы ответить на запрос [L, R], найдите последнюю версию дерева сегментов, чтобы обновление происходило до R. Если вы выполняете бинарный поиск по версиям, это занимает O(log N) времени.

В версии дерева сегментов рассматриваются только пассажиры с левой конечной точкой

Источник

Утверждение:

Вход: list<x',x'',Y>

Ввод запроса: (X',X'')

Выход: Ymin

Ограничения:

1 ≤ Q, S, m ≤ 10^5
1 ≤ N ≤ 10^9

Time: 1s
Memory: 256 Mb

Ответ:

Метод структуры данных вы можете использовать:

1. Грубая сила: непосредственно итерировать список и выполнить проверку.

2. Сортировка: сортировка списка по Y [от низшего к высшему], а затем переберите его.

Примечание: сортировка большого списка займет много времени.

Sort on Y
Ymin = -1                                            //Maintain Ymin
for i[0 : len(input)] :                              //Iterate through tuples
    if Ymin != -1 && Y(i-1) != Yi : return Ymin      // end case
    else if x' > X'' : Ymin = Yi                     //its on right of query tuple
    else if x'<X' && (x' + length <= X') : Ymin = Yi //on left of query tuple
    else next

3. Hashmap: Map<Y, list< tuple<x',length> > > хранить список строк для каждого Y и перебирать их, чтобы получить как минимум Y,

Примечание: потребуется дополнительное время для построения карты.

Iterate through list and build a Map 
Iterate through Map keys :
    Iterate through list of tuples, for each tuple :
        if x' > X'': Continue                            //its on right of query tuple
        else if x'<X' && (x' + length <= X') :  return Y //on left of query tuple
            else next Y

4. Матрица: вы можете построить матрицу с 1 для занятой точки и 0 для пустой.

Примечание: для сборки матрицы потребуется дополнительное время, а итерация по матрице занимает много времени, поэтому бесполезна.

Пример:

    0 1 1 1 0 0 
    1 1 0 1 0 0
    0 1 1 1 1 0
Источник
Другие вопросы по тегам