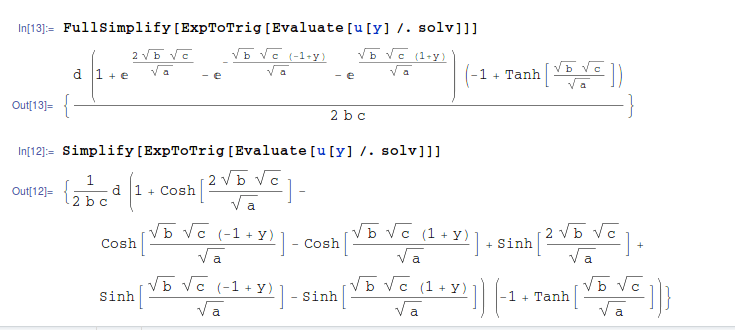Решение дифференциального уравнения в Mathematica

Question

У меня есть проблема синтаксиса решения дифференциального уравнения в Mathematica (10-я версия).

Вход для уравнения, которое мне нужно решить, выглядит следующим образом:

solv = DSolve[{ a*u''[y] - b*u[y] == d, u'[0] == 0, u[1] == 0}, u, {y, -1, 1}]

Который после использования ExpToTrig и FullSimplify я получаю ответ, который я ищу:

(d (-1 + Cosh[(Sqrt[b] y)/Sqrt[a]] Sech[Sqrt[b]/Sqrt[a]]))/b

Однако моя проблема возникает, когда я хочу поместить больше коэффициентов в уравнение. Например:

solv = DSolve[{ a* u''[y] - b* c* u[y] == d, u'[0] == 0, u[1] == 0}, u, {y, -1, 1}]

На этот раз я получаю за:

FullSimplify[ExpToTrig[Evaluate[u[y] /. solv]]]

Следующий ответ:

(d (1 + E^((2 Sqrt[b] Sqrt[c])/Sqrt[a]) - E^(-((Sqrt[b] Sqrt[c] (-1 + y))/Sqrt[a])) - E^((Sqrt[b] Sqrt[c] (1 + y))/Sqrt[a])) (-1 + Tanh[(Sqrt[b] Sqrt[c])/Sqrt[a]]))/(2 b c)

Вместо этого, когда я объединяю b и c (подставьте: bc = b * c):

solv = DSolve[{ a*u''[y] - bc*u[y] == d, u'[0] == 0, u[1] == 0}, u, {y, -1, 1}]

Я получил:

(d (-1 + Cosh[(Sqrt[bc] y)/Sqrt[a]] Sech[Sqrt[bc]/Sqrt[a]]))/bc

В моем случае я не могу просто заменить, потому что слишком много уравнений и некоторые параметры (коэффициенты) отменяются.

Спасибо!

Answer 1

Ваша проблема с FullSimplify, Это считает exp форма более "простая", чем форма триггера, так что это уничтожает то, что ExpToTrig делается. Используя только Simplify на его месте будет поддерживать ExpToTrig преобразование. Моя быстрая попытка ниже показывает сравнение.