Локальная интерполяция высшего порядка неявных кривых в Python

Учитывая набор точек, описывающих некоторую траекторию в 2D-плоскости, я хотел бы обеспечить плавное представление этой траектории с локальной интерполяцией высокого порядка.

Например, скажем, мы определяем круг в 2D с 11 точками на рисунке ниже. Я хотел бы добавить точки между каждой последовательной парой точек по порядку или произвести плавный след. Добавление точек на каждом сегменте достаточно просто, но оно создает разрывы наклона, типичные для "локальной линейной интерполяции". Конечно, это не интерполяция в классическом смысле, потому что

  • функция может иметь несколько y значения для данного x
  • было бы просто добавить больше точек на траектории (непрерывное представление не требуется).

так что я не уверен, что будет правильным словарным запасом для этого.

GPS-траектория

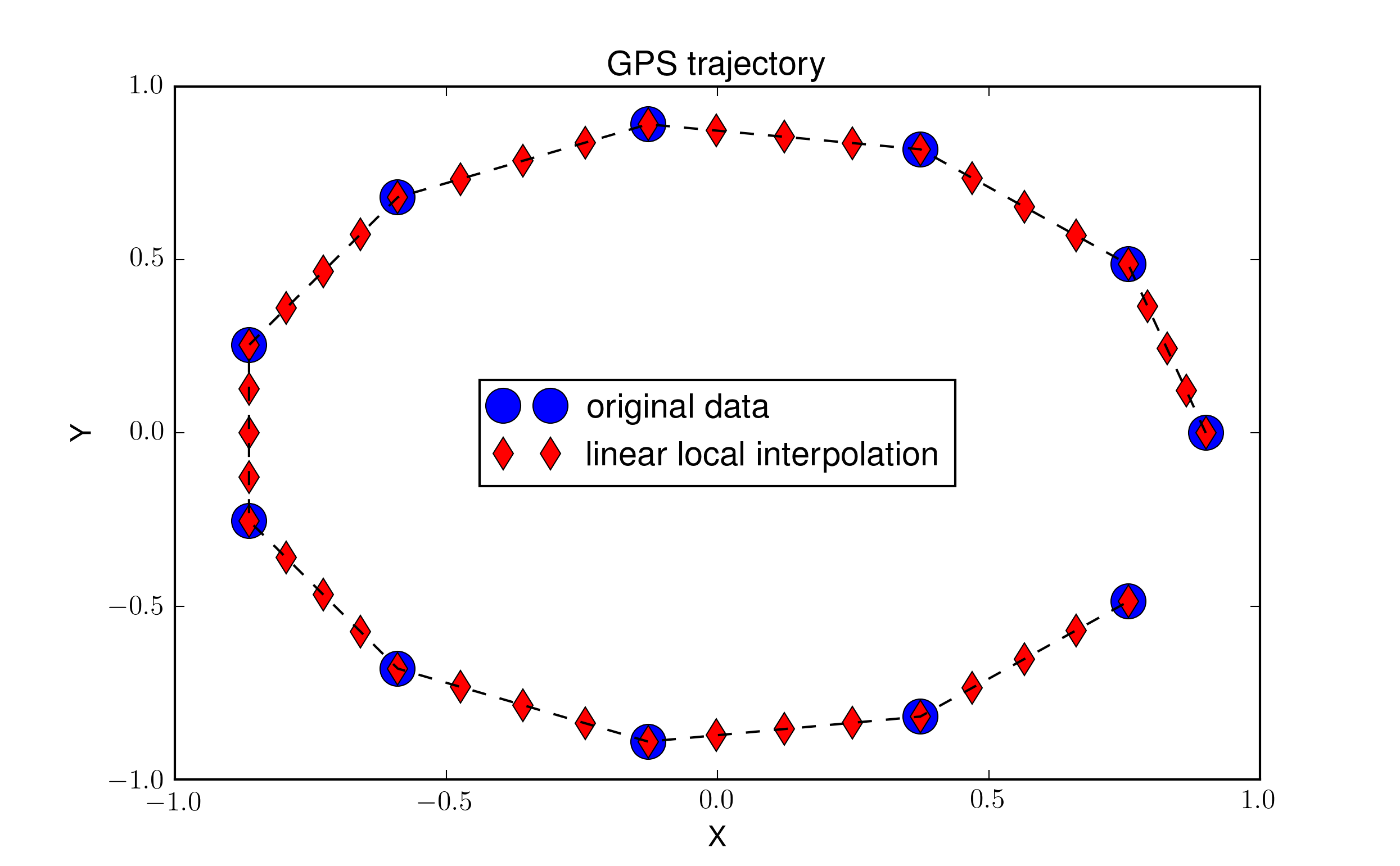
Код для создания этой фигуры можно найти ниже. Линейная интерполяция выполняется с lin_refine_implicit функция. Я ищу решение более высокого порядка для получения плавного следа, и мне было интересно, есть ли способ достичь его с помощью классических функций в Scipy? Я пытался использовать различные 1D интерполяции из scipy.interpolate без особого успеха (опять же из-за нескольких y значения для данного x).

Конечная цель состоит в том, чтобы использовать этот метод, чтобы обеспечить плавную траекторию GPS из дискретных измерений, поэтому я думаю, что у этого должно быть где-то классическое решение.

import numpy as np
import matplotlib.pyplot as plt

def lin_refine_implicit(x, n):
    """
    Given a 2D ndarray (npt, m) of npt coordinates in m dimension, insert 2**(n-1) additional points on each trajectory segment
    Returns an (npt*2**(n-1), m) ndarray
    """
    if n > 1:
        m = 0.5*(x[:-1] + x[1:])
        if x.ndim == 2:
            msize = (x.shape[0] + m.shape[0], x.shape[1])
        else:
            raise NotImplementedError

        x_new = np.empty(msize, dtype=x.dtype)
        x_new[0::2] = x
        x_new[1::2] = m
        return lin_refine_implicit(x_new, n-1)
    elif n == 1:
        return x
    else:
        raise ValueError
n = 11
r = np.arange(0, 2*np.pi, 2*np.pi/n)
x = 0.9*np.cos(r)
y = 0.9*np.sin(r)
xy = np.vstack((x, y)).T
xy_highres_lin = lin_refine_implicit(xy, n=3)

plt.plot(xy[:,0], xy[:,1], 'ob', ms=15.0, label='original data')
plt.plot(xy_highres_lin[:,0], xy_highres_lin[:,1], 'dr', ms=10.0, label='linear local interpolation')
plt.legend(loc='best')
plt.plot(x, y, '--k')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('GPS trajectory')
plt.show()
Источник

2 ответа

Решение

Это называется параметрической интерполяцией.

scipy.interpolate.splprep предоставляет сплайн-аппроксимации для таких кривых. Это предполагает, что вы знаете порядок, в котором точки находятся на кривой.

Если вы не знаете, какая точка наступает после какой на кривой, проблема становится более сложной. Я думаю, что в этом случае проблема называется многократным обучением, и некоторые из алгоритмов в scikit-learn могут быть полезны в этом.

Источник

Я бы посоветовал вам попытаться преобразовать ваши декартовы координаты в полярные координаты, что должно позволить вам использовать стандартные scipy.interpolation без проблем, поскольку у вас больше не будет неоднозначности отображения x->y.

Источник
Другие вопросы по тегам