Не могу понять, как работает растяжка

Question

Я не могу понять, как работает splaying.
Часть, которой я не могу следовать, - это то, как мы узнаем, если: zig II) zig-zag или iii) zig-zig должно быть сделано.
Если я правильно понимаю, это связано с текущим узлом в пути.
Если это ребенок корня, то это zig в противном случае либо (ii), либо (iii) в зависимости от того, являются ли родительский элемент текущего узла и текущий узел левым (или правым) потомком. Хорошо, пока.
Теперь часть, которую я не получаю:
По мере того, как мы движемся вниз, разве не происходит процесс "удаления" промежуточных узлов в левое и правое поддеревья, чтобы у нас было среднее дерево, которое в конечном итоге будет корнем искомого элемента?
Тогда, если мы начнем с дерева, мы будем делать постоянно zig и ничего больше, так как мы удаляем элементы и всегда в корне.
Пример: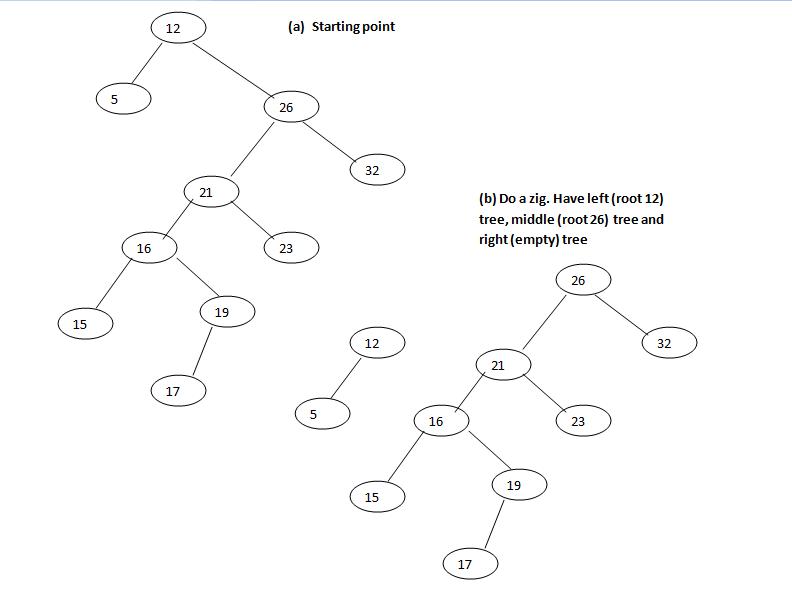

Если, например, я ищу 20 Я бы начал с корня и пошел налево. Таким образом, текущий узел имеет root в качестве родителя, а я делаю zig. Что теперь происходит?? я в 26 и идти налево, но не 26 тоже рут? Так я должен заниматься зигом?
Но из того, что я вижу в этом примере, делается зигзаг, и я не могу понять, почему.
Любая помощь здесь?

Answer 1

Под корнем они подразумевают корень всего дерева, а не корень поддерева, которое вы распространяете. Итак, в вашем примере 12 является корнем всего дерева.

...

Если вы хотите, чтобы пример работал, я недавно написал код SplayTree на Java. Вы можете найти код здесь.

Главное, что есть в Splay Tree, это то, что они перемещают последний вставленный / запрошенный узел вверх (максимум) на два уровня в дереве. Вы должны выполнить зиг, зиг-зиг или зигзаг в зависимости от расположения его родительских и родительских узлов.

При обращении к узлу x на x выполняется операция расширения, чтобы переместить его в корень. Чтобы выполнить операцию воспроизведения, мы выполняем последовательность шагов воспроизведения, каждый из которых перемещается на х ближе к корню.

Три типа шагов воспроизведения: (g = родительский элемент, p = родительский элемент и x = узел для отображения)

• Шаг Zig: этот шаг выполняется, когда p является корнем. Дерево вращается по краю между x и p.
• Шаг Zig-Zig: Этот шаг выполняется, когда p не является корнем, а x и p либо правые, либо левые. Дерево вращается на ребре, соединяющем p с его родителем g, затем вращается на ребре, соединяющем x с p.
• Шаг зигзага: этот шаг выполняется, когда p не является корнем, а x является правым дочерним элементом, а p является левым дочерним элементом или наоборот. Дерево вращается на ребре между x и p, затем вращается на ребре между x и его новым родителем g.

http://en.wikipedia.org/wiki/Splay_tree

Ниже приведено отображение узла 3 в дереве.

Дерево перед расплескиванием:

└── 0
    └── (right) 9
        └── (left) 7
            ├── (left) 5
            │   ├── (left) 1
            │   │   └── (right) 2
            │   │       └── (right) 4
            │   │           └── (left) 3
            │   └── (right) 6
            └── (right) 8

После (справа-> слева) зигзага к узлу 3.

└── 0
    └── (right) 9
        └── (left) 7
            ├── (left) 5
            │   ├── (left) 1
            │   │   └── (right) 3
            │   │       ├── (left) 2
            │   │       └── (right) 4
            │   └── (right) 6
            └── (right) 8

После другого (влево-> вправо) зигзага к узлу 3.

└── 0
    └── (right) 9
        └── (left) 7
            ├── (left) 3
            │   ├── (left) 1
            │   │   └── (right) 2
            │   └── (right) 5
            │       ├── (left) 4
            │       └── (right) 6
            └── (right) 8

После (слева-> слева) Zig-Zig до узла 3.

└── 0
    └── (right) 3
        ├── (left) 1
        │   └── (right) 2
        └── (right) 7
            ├── (left) 5
            │   ├── (left) 4
            │   └── (right) 6
            └── (right) 9
                └── (left) 8

После (справа) Zig к узлу 3. Теперь время остановиться, так как 3 находится в корневой позиции.

└── 3
    ├── (left) 0
    │   └── (right) 1
    │       └── (right) 2
    └── (right) 7
        ├── (left) 5
        │   ├── (left) 4
        │   └── (right) 6
        └── (right) 9
            └── (left) 8t) 6
                └── (right) 9
                    └── (left) 8

Если вы попытаетесь снова получить доступ к узлу 3 в Дереве, его не нужно будет отображать, поскольку он уже находится в корневом положении.