Создать окно Хэмминга длиной 64 с перекрытием 60% в Matlab

Question

Я пытаюсь отдать за окно распределения Вигнера-Вилле Хэмминга длины 64 с перекрытием 60% здесь. Я могу создать окно Хэмминга длиной 64

h=hamming(64);

Вот несколько теоретических советов по этому вопросу. Окно, кажется, является своего рода сверткой трех волн Хэмминга с 60% вероятностью свертки.

Перекрытие, по-видимому, является своего рода сверткой трех функций. Моя попытка для трех окон и их перекрытий

conv(conv(hamming(64), hamming(64)), conv(hamming(64), hamming(64)))

Моя попытка для двух окон и их перекрытий

h = conv(hamming(64), hamming(64));

Оба результата, кажется, не дают мне лучших результатов по распределению Вигнера-Вилле. Многие облачные пики все еще видны. Таким образом, ключ, кажется, разделяет окна во времени, так как текущий результат оконной функции возвращает точно такое же изображение, как только в окне Хемминга (64).

Думая, что 60% перекрываются

Размеры hamming(64) 64x1, в то время как conv(hamming(64), hamming(64)) 127x1 двухместный Сделать вероятностный алгоритм с вероятностью 60% непросто, потому что мы не можем итерировать обе функции линейно.

Как вы можете создать окно Хэмминга с перекрытием 60%?

Answer 1

Быстрый поиск указанного буфера может стоить попытки.

h = hamming(64);
y = buffer(h, 1, floor(64 * 0.6));

Но моя версия Matlab не поддерживает эту функцию, поэтому я не пытался.

Answer 2

Основано на комментарии Флориса. Запустите распределение Вигнера-Вилле с перекрытием 60% окна Хемминга 64.

h = hamming(64);
h2 = hamming(38);
h = conv(h, h2);
[B,T,F] = tfrwv(data, 1:length(data), length(data), h);

Изображение выглядит точно так же, как с окном Хэмминга-64. Картинка не должна быть одинаковой, так как вектор Хемминга-64 и эта оконная функция отличаются по значениям. Поэтому, вероятно, следует изучить норму, чтобы оценить вещь.

log(abs(data)) дает на левой стороне, в то время как оригинал на правой стороне

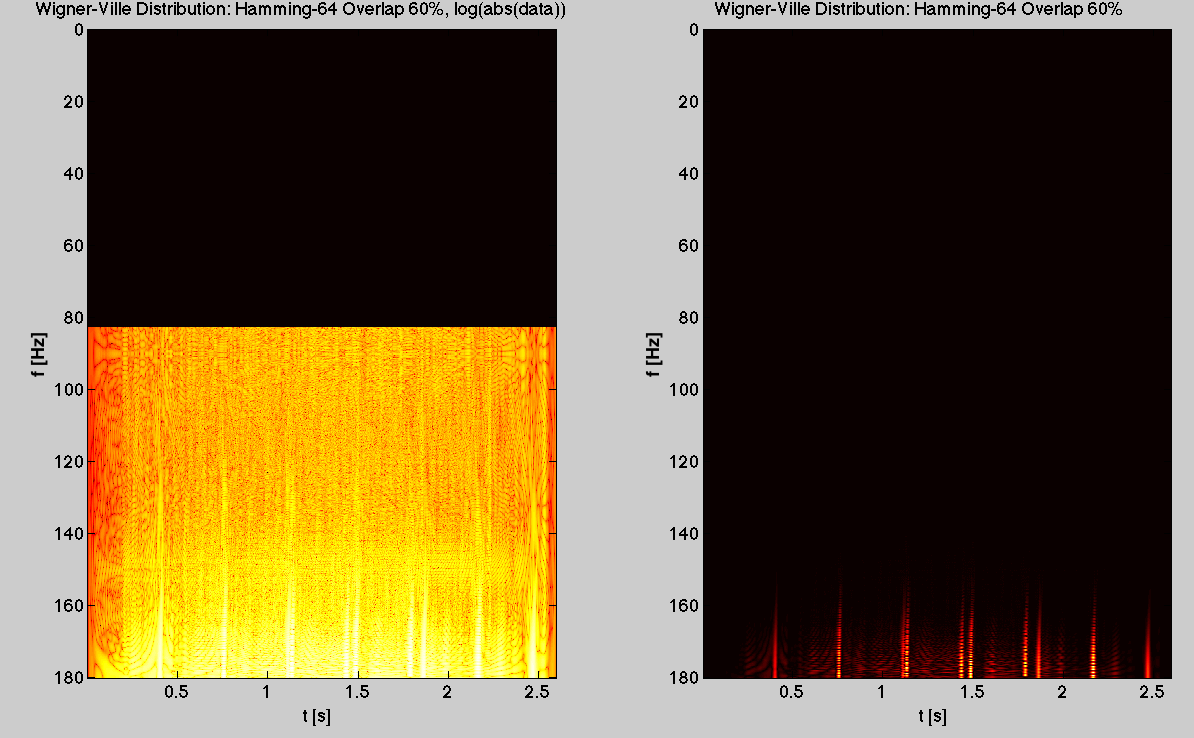
Здесь и сейчас логарифмическая функция применяется к распределению с Хеммингом 64 и к другому с Хеммингом 64, но с перекрытием 60%

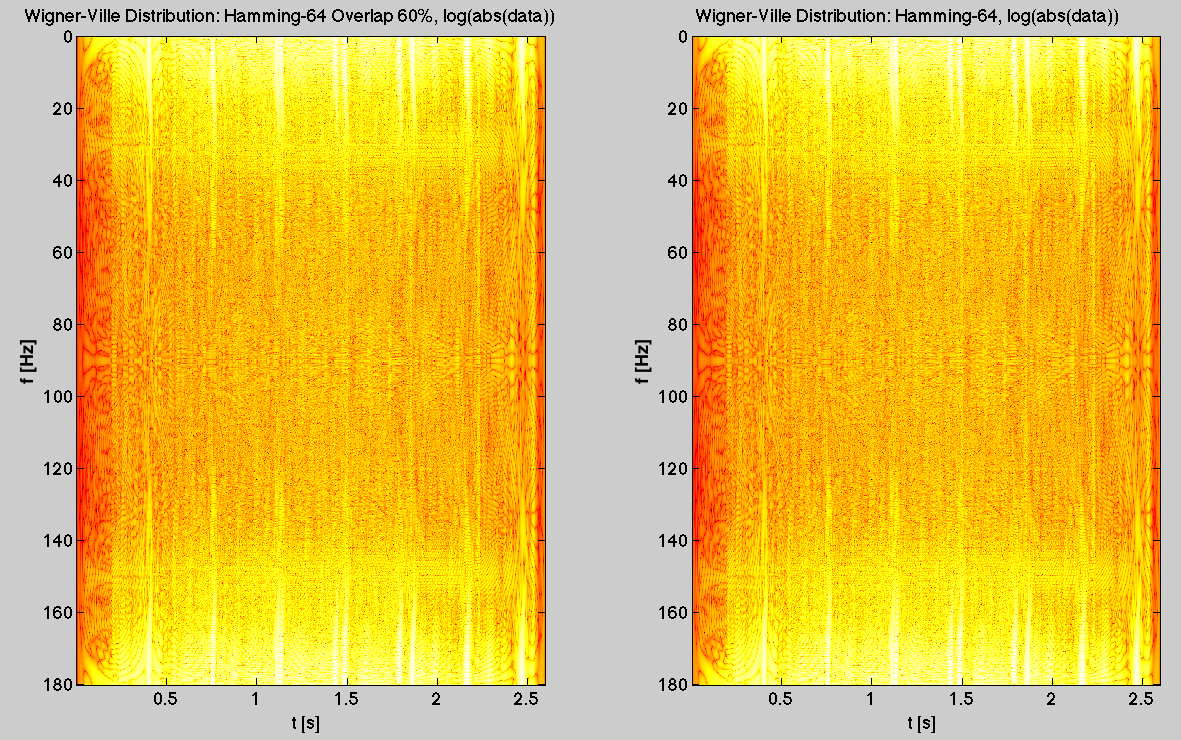
После логарифмической функции изображения выглядят одинаково.