Как работают Суффикс-деревья?

Question

Я просматриваю главу о структурах данных в Руководстве по разработке алгоритмов и наткнулся на деревья суффиксов.

Пример гласит:

Входные данные:

XYZXYZ$
 YZXYZ$
  ZXYZ$
   XYZ$
    YZ$
     Z$
      $

Выход:

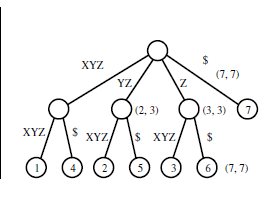
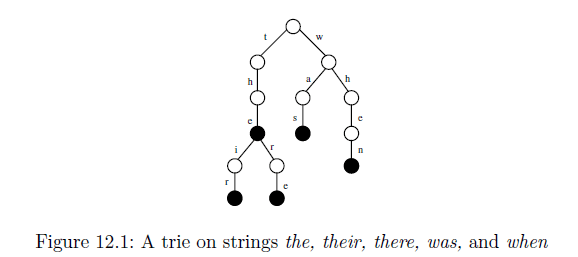
Я не могу понять, как это дерево генерируется из заданной входной строки. Суффиксные деревья используются для поиска данной Подстроки в данной Строке, но как данное дерево помогает в этом? Я понимаю другой приведенный ниже пример дерева, показанного ниже, но если приведенное ниже дерево будет сжато до дерева суффиксов, то как бы это выглядело?

Answer 1

Стандартные эффективные алгоритмы построения суффиксного дерева определенно нетривиальны. Основной алгоритм для этого называется алгоритмом Укконена и представляет собой модификацию простого алгоритма с двумя дополнительными опциями. Возможно, вам лучше прочитать этот предыдущий вопрос, чтобы узнать, как его построить.

Вы можете построить суффиксные деревья, используя стандартные алгоритмы вставки в radix, пытаясь вставить каждый суффикс в дерево, но для этого потребуется время O (n²), что может быть дорого для больших строк.

Что касается быстрого поиска по подстроке, помните, что дерево суффиксов - это сжатый набор всех суффиксов исходной строки (плюс некоторый специальный маркер конца строки). Если строка S является подстрокой исходной строки T и у вас есть три всех суффиксов T, то вы можете просто выполнить поиск, чтобы увидеть, является ли T префиксом какой-либо из строк в этом дереве. Если это так, то T должна быть подстрокой S, поскольку все ее символы существуют в некоторой последовательности где-то в T. Алгоритм поиска подстрок дерева суффиксов - это именно такой поиск, применяемый к сжатому дереву, где вы следуете за соответствующими ребрами на каждом шаге.

Надеюсь это поможет!

Answer 2

Я не могу понять, как это дерево генерируется из заданной входной строки.

По сути, вы создаете трилистику со всеми указанными вами суффиксами. При вставке в поле patricia, вы ищите в корне дочерний элемент, начиная с первого символа из входной строки, если он существует, вы продолжаете вниз по дереву, но если этого не происходит, вы создаете новый узел вне корня. Корень будет иметь столько же дочерних элементов, сколько уникальных символов во входной строке ($, a, e, h, i, n, r, s, t, w). Вы можете продолжить этот процесс для каждого символа во входной строке.

Суффиксные деревья используются для поиска данной Подстроки в данной Строке, но как данное дерево помогает в этом?

Если вы ищете подстроку "курица", то начните поиск в корне дочернего элемента, который начинается с "h". Если длина строки в дочернем "h", то продолжайте обрабатывать дочерний "h", пока не дойдете до конца строки или не получите несоответствие символов во входной строке и дочерней "h" строке. Если вы соответствуете всем дочерним элементам "h", то есть ввод "hen" соответствует "he" в дочерних "h", переходите к дочерним элементам "h", пока не получите "n", если не удается найти дочерний элемент с "n" подстрока не существует.

Компактный суффикс-код Trie:

└── (black)
    ├── (white) as
    ├── (white) e
    │   ├── (white) eir
    │   ├── (white) en
    │   └── (white) ere
    ├── (white) he
    │   ├── (white) heir
    │   ├── (white) hen
    │   └── (white) here
    ├── (white) ir
    ├── (white) n
    ├── (white) r
    │   └── (white) re
    ├── (white) s
    ├── (white) the
    │   ├── (white) their
    │   └── (white) there
    └── (black) w
        ├── (white) was
        └── (white) when

Suffix Tree code:

String = the$their$there$was$when$
End of word character = $
└── (0)
    ├── (22) $
    ├── (25) as$
    ├── (9) e
    │   ├── (10) ir$
    │   ├── (32) n$
    │   └── (17) re$
    ├── (7) he
    │   ├── (2) $
    │   ├── (8) ir$
    │   ├── (31) n$
    │   └── (16) re$
    ├── (11) ir$
    ├── (33) n$
    ├── (18) r
    │   ├── (12) $
    │   └── (19) e$
    ├── (26) s$
    ├── (5) the
    │   ├── (1) $
    │   ├── (6) ir$
    │   └── (15) re$
    └── (29) w
        ├── (24) as$
        └── (30) hen$

Answer 3

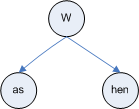
Дерево суффиксов в основном просто сжимает серии букв, когда нет выбора, который нужно сделать. Например, если вы посмотрите на правую сторону дерева в вашем вопросе, после того как вы увидели wНа самом деле есть только два варианта: was а также when, В три, as в was и hen в when у каждого все еще есть один узел для каждой буквы. В дереве суффиксов вы сложите их в два узла, as а также henТаким образом, правая сторона вашего дерева превратится в: