Интерпретация первых нескольких компонентов PCA для распознавания рукописных цифр
Поэтому в Matlab я выполняю PCA на рукописных цифрах. По сути, я имею в виду 30*30 размерных изображений, то есть 900 пикселей, и после PCA я рассматриваю компоненты, которые фиксируют большую часть дисперсии, скажем, первые 80 основных компонентов (ПК), основанные на некотором пороговом значении. Теперь эти 80 ПК также имеют размерность 900, и когда я строю их с помощью imshow, я получаю несколько изображений, например, что-то вроде 0, 6, 3, 5 и т. Д. Какова интерпретация этих первых нескольких ПК (из из 80 я извлек)?
2 ответа
Сначала немного о номенклатуре: PCA находит собственные векторы ковариационной матрицы данных, а затем преобразует данные в основу собственных векторов. Результат этой операции состоит из двух частей: преобразованные данные и собственные векторы, используемые для преобразования. Обычно это первое, что называется главными компонентами (ПК). Для второго нет установленного названия, но мне нравится термин главные режимы (PM). Ваш вопрос о толковании PM.
Интерпретация PM, как правило, сложная, если не невозможная. Конечно, они имеют простую техническую интерпретацию, PCA ищет направления в пространстве данных, вдоль которых происходит максимальное количество вариаций, и PM являются этими направлениями. Для первого компонента это максимизация бесплатна и охватывает основное направление, по которому происходит изменение. Более поздние компоненты вынуждены быть ортогональными к предыдущим, что часто приводит к появлению все более сложных высокочастотных паттернов, которые все труднее и труднее интерпретировать.
В случае вашего набора данных ситуация может отличаться, потому что он, вероятно, имеет некую структуру кластера в очень многомерном пространстве, где кластеры соответствуют цифрам 0–9. Было отмечено, что в таком случае существует слабое соответствие между PCA и кластеризацией k-средних, так что первые PM стремятся восстановить пространство, охватываемое центроидами кластера. В этом случае первые PM будут представлять собой комбинации кластерных центроидных паттернов, возможно, даже приблизительно совпадающих с этими паттернами. Я думаю, это то, что объясняет ваше наблюдение.
Больше информации в ответ на комментарии ОП:
Приведенный выше фрагмент Википедии относится к Ding and He (2004), K-означает кластеризация посредством анализа основных компонентов (ссылка). Они пишут в аннотации: "Здесь мы доказываем, что основными компонентами являются непрерывные решения индикаторов дискретного членства в кластере для кластеризации K-средних". Насколько я понимаю, это означает, что "загрузка компонента", значение основного компонента для данной точки данных связана или, по крайней мере, связана с показателем того, принадлежит ли эта точка данных к кластеру. Они продолжают: "Эквивалентно, мы показываем, что подпространство, охватываемое центроидами кластера, задается спектральным расширением ковариационной матрицы данных, усеченной в терминах K - 1". Это означает, что подпространство пространства данных (в вашем случае 900-мерное), которое охватывает первые K - 1 главные моды (собственные векторы), является или близко к пространству, охватываемому (различием) центроидов кластера (среднее изображение для каждой цифры). Если это так, большая часть межкластерной дисперсии фиксируется этими первыми основными компонентами.
Подумайте об этом следующим образом: PCA позволяет сократить 900 измерений данных примерно до 10 измерений, восстанавливая все изображения 30x30 из набора из 10 "типичных" изображений 30x30. Это означает, что каждое изображение может быть приблизительно закодировано 10 числами вместо 900 чисел. Чтобы это было возможно, "типичные" изображения должны быть похожи на то, как в среднем выглядят "0", "1" и т. Д. В простейшем случае 10 изображений могут быть просто средним значением "0", средним значением "1" и т. Д. Обычно это не так, но может быть и так. Это помогает? Я думаю, что "0" соответствует сильнейшему ПК.
PCA извлекает наиболее важную информацию из набора данных и сжимает размер набора данных, сохраняя только важную информацию - главные компоненты.
Первый главный компонент построен таким образом, что он имеет наибольшую возможную дисперсию. Второй компонент вычисляется при условии, что он ортогонален первому компоненту и имеет наибольшую возможную дисперсию.
В вашем случае данные представляют собой набор изображений. Допустим, у вас есть 1000 изображений, и вы вычисляете первые пять основных компонентов (5 изображений, построенных по алгоритму PCA). Вы можете представить любое изображение в виде 900 точек данных (30x30 пикселей) или путем комбинации 5 изображений с соответствующими коэффициентами miltiplication.
Цель алгоритма PCA состоит в том, чтобы сконструировать эти 5 изображений (главных компонентов) таким образом, чтобы изображения в вашем наборе данных были представлены наиболее точно с помощью комбинации заданного числа основных компонентов.
ОБНОВИТЬ:
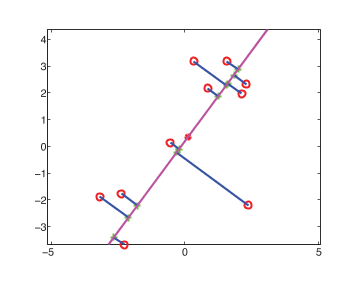
Посмотрите на изображение ниже (из удивительной книги Кевина Мерфи). Изображение показывает, как точки в 2 измерениях (красные точки) представлены в 1 измерении (зеленые крестики), проецируя их на вектор (фиолетовая линия). Вектор является первым главным компонентом. Цель PCA состоит в том, чтобы построить эти векторы, чтобы минимизировать ошибку восстановления. В вашем случае эти векторы могут быть представлены в виде изображений.
Вы можете обратиться к этой статье для получения более подробной информации об использовании PCA для распознавания рукописных цифр.