Видимо случайная векторная графика: ТСНЭ

Question

Я успешно создал векторную модель, используя библиотеку Gensim's word2vec. Расстояние между связанными векторами хорошее (то есть, что производное сходство имеет смысл с человеческой точки зрения).

Однако попытка отобразить эти векторы на графе оказалась сложной задачей. Естественно, N-размеры векторов должны быть уменьшены, чтобы их можно было построить на графике: и для этого я использовал TSNE.

import gensim, logging, os
import codecs
import numpy as np
import matplotlib.pyplot as plt
import gensim, logging, os
from sklearn.manifold import TSNE

wvs = model.syn1neg
vocabulary = model.wv.vocab


tsne = TSNE(n_components=2, random_state=0)
np.set_printoptions(suppress=True)
Y = tsne.fit_transform(wvs[::])

plt.scatter(Y[:, 0], Y[:, 1])
for label, x, y in zip(vocabulary, Y[:, 0], Y[:, 1]):
    plt.annotate(label, xy=(x, y), xytext=(0, 0), textcoords='offset points')
plt.show()

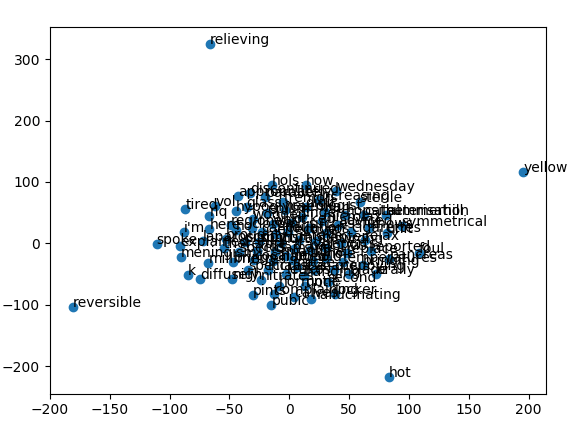
Однако результирующие точки, относящиеся к векторам, кажутся по существу случайными - есть только один огромный кластер с парой выбросов.

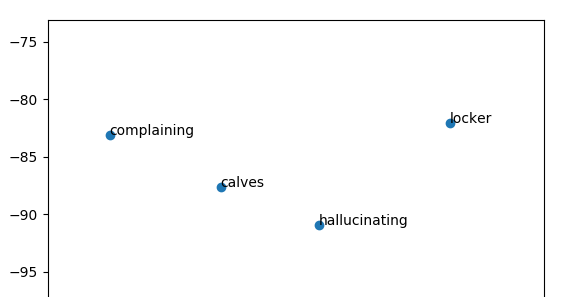
Показательный пример: обратите внимание на то, что ближайшие соседи "галлюцинируют" на краю скопления

Но фактические векторы вернули usng model.most_simil ()

[("взволнованный", 0,7707732319831848), ("беспокойный", 0,740711510181427), ("дезориентированный", 0,7242116332054138), ("сбитый с толку", 0,7215688228607178), ("агрессивный", 0,71 69249057769775), 0,665 (0,65), 0,665, сингл. ("слезный", 0,6573441624641418), ("агитированный", 0,6566967964172363), ("сонный", 0,6562871932983398), ("встряхивающий", 0,6419488191604614)]

Каким образом я могу начать подходить к этому, чтобы попытаться сделать вывод более осмысленным?

Answer 1

Абсолютно прочитайте статью, на которую ссылается @MattiLyra. Кроме того, основываясь на том, что я знаю (не видя фактических данных), вы можете увеличить n_iter параметр хороший бит. Обычно 1000 итераций не приведут вас в статическое состояние. Кроме того, вы также можете поиграть с method параметр. Документация для sklearn.manifold.TSNE состояния:

"По умолчанию алгоритм вычисления градиента использует приближение Барнса-Хата, работающее за время O(NlogN). Method= 'точный' будет выполняться с более медленным, но точным алгоритмом за время O(N^2). Должен использоваться точный алгоритм когда ошибки ближайшего соседа должны быть лучше, чем 3%. Однако точный метод не может масштабироваться до миллионов примеров ".

Если вы измените метод на "точный", вы можете использовать n_iter_without_progress параметр и в основном позволяют модели найти статическую точку.