Понимание грамматики ETF и абстрактных синтаксических деревьев

Question

Я приложил проблему ниже с ответом. Моя проблема в том, что я не могу этого понять. Можете ли вы дать общее объяснение в деталях о деревьях разбора и грамматике ETF, выведя первое выражение?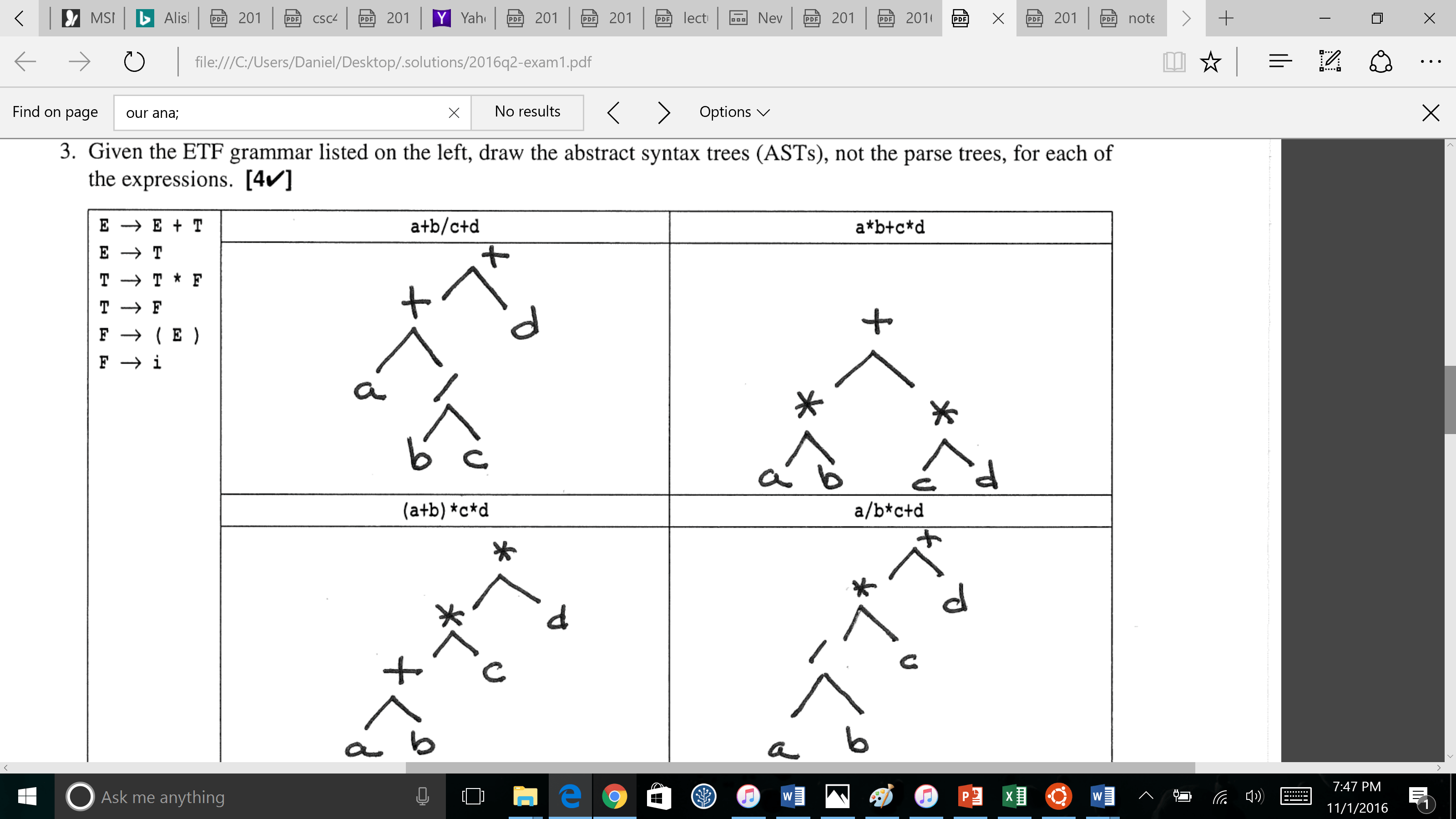

Просто попробуйте объяснить первое выражение, a + b / c + d. Я думаю, что это не так сложно, но я просто не смог найти подходящих ресурсов, чтобы понять это. Можете ли вы также предоставить ресурсы, которые объясняют грамматику ETF? Если вы не хотите давать объяснения, было бы неплохо, если бы вы хотя бы могли указать какой-то ресурс, чтобы это понять. Как стратегия, я думаю, что лучше сначала построить дерево разбора, а затем преобразовать его в AST.

Answer 1

Это неосторожный вопрос. Априори нет причин, по которым грамматика ETF должна соответствовать какому-либо конкретному AST. Это правда, что для синтаксического анализатора, основанного на грамматике EFT, проще всего построить AST с обычными правилами приоритета. Также верно и то, что подобная леворекурсивная грамматика облегчает реализацию левоассоциативных операций в AST.

Но это большие предположения, которые следует сформулировать в явном виде. Чтобы полностью определить проблему, вам нужно дать атрибутную грамматику, которая производит AST, а не просто голую грамматику.

Грамматика атрибута будет указывать, как строятся узлы AST:

E_a -> E_b + T  { E_a.ast = makeNode('+', E_b.ast, T.ast) }
E -> T          { E.ast = T.ast }
...
F -> i          { F.ast = makeLeaf(i) }

Таким образом, если мы сделаем предположение о типичной грамматике атрибута, то структура грамматики EFT подразумевает приоритет операций.

Оператор в верхней части грамматики, полученный непосредственно из начального символа, соответствует наименьшему приоритету. Вы можете думать об этом так:

E -> E + T | T

расширяется до списка из одного или нескольких TErms разделены + операторы.

E -> T + ... + T

Это подразумевает, что грамматика атрибута создает перекошенное дерево терминов (Tс). Все, что происходит "в Ts"выше в приоритете. Эти вещи" связаны друг с другом ", не заботясь об окружающей +,

Соответствующий AST будет выглядеть так:

+
| \
+  T
| \
+  T
|
.
.
.
+
| \
T  T

Словом, выражение представляет собой сумму предыдущих терминов (левое поддерево под корнем), добавленных к последнему члену (правое поддерево). Последовательные дополнения происходят слева направо. Это называется левой ассоциативной операцией. Некоторые операции - например, возведение в степень - например, дерево перекошено в другую сторону, поэтому операции оцениваются справа налево. 2^3^2 означает "2 в 9-й степени" = 512, а не "8 в квадрате" = 64.

Теперь вы можете расширить условия. В вашем примере первый термин, наконец, расширяется до a, Второй расширяется до F / F и, наконец, b / c, (Это предполагает, что * правило распространяется на / а также.) Третий член расширяется до d, Таким образом, вы в конечном итоге

+
| \
+  T
| \
T  T

и это становится

+__
|  \
+   d
| \  
a  /  
   |\
   b c

Операция b/c имеет более высокий приоритет, чем + потому что это ближе к листьям дерева.

Скобки отвергают этот естественный приоритет. Выражение

(a + b) / c

расширяется изначально только с одним термином!

E -> T
  -> T / F
  -> F / F

Второй фактор касается c, Итак, интуитивно, дерево имеет форму:

/
| \ 
F  c

Теперь ключевое правило атрибута грамматики для расширения F является

F -> ( E )  { F.ast = E.ast }

Так что у нас действительно есть

/_______
|       \
( E )    c

Сейчас ( E ) расширяется до AST для a + b все само по себе

/_______
|       \
+        c
| \ 
a  b

Обратите внимание, как + ближе к листьям. Скобки дали ему более высокий приоритет, чем /!