Комбинации "продуктов" для формирования стимулирования сбыта

Question

Я перерабатываю унаследованную систему, которая объединяет корзину выбранных пользователем розничных продуктов в одну или несколько действительных рекламных акций. Эти акции являются отраслевым стандартом BOGOF (купи одно, получи одно бесплатно), купи два, получи третье бесплатно, купи товары X и Y и получи скидку 10% и т. Д., Но все они требуют, чтобы вы могли отфильтровать список потенциальных предметов по этим которые удовлетворяют этим акциям.

Я хотел бы, чтобы решение состояло в том, чтобы взять всю корзину розничных товаров и проанализировать их за одну операцию, в отличие от действующего метода сопоставления одного товара с моментом его заказа. (Текущее решение приводит к нежелательным ограничениям)

Каждое продвижение имеет ряд соответствующих продуктов, которые должны присутствовать, чтобы запустить продвижение. Они расположены в количестве n наборов (или позиций), например:

Example "Buy two get third free" Promotion =

| Item 1 |             | Item 1 |             | Item 2 |
|   or   |             |   or   |             |   or   |
| Item 2 |     AND     | Item 4 |     AND     | Item 6 |
|   or   |             |   or   |             |   or   |
| Item 3 |             | Item 9 |             | Item 4 |

  Set 1                   Set 2                  Set 3

Каждое рекламное предложение должно содержать ровно один товар из каждой группы, если только товар не появляется в одном и том же наборе несколько раз. Акция может иметь неограниченный (но обычно < 10) "набор" продуктов.

В качестве простого примера, корзина покупок Item 1, Item 4 and Item 6 вызовет продвижение, аналогично корзина Item 1, Item 1 and Item 2 также вызовет это. Однако корзина Item 1, Item 2 and Item 3 не будет, так как каждый набор не выполняется.

Помимо неясного вопроса о том, как лучше всего определить, когда была инициирована рекламная акция, мне также потребуется восстановить набор (позицию), с которой был сопоставлен товар, для обработки детализации цены и т. Д. Также было бы желательно если более дорогие (в денежном выражении) товары предпочтительнее, чем менее дорогие (с одинаковым соответствием), при назначении их для продвижения

---

Надеюсь, что следующая часть поможет найти решение, не настолько ясное, что оно создаст ненужный шум, не стесняйтесь игнорировать!

Мое лучшее решение на данный момент - создать новый набор для каждой розничной позиции в "корзине покупок", содержащей набор (позицию) продвижения, который будет удовлетворять этот элемент. то есть.

Item 1 satisifies sets: {1,2}
Item 4 satisifies sets: {2,3}
Item 6 satisifies sets: {3}

Тогда моя теория состоит в том, что вы "проверяете", что этот список наборов содержит уникальный элемент в каждой позиции и что каждая позиция продвижения заполнена. До сих пор все мои рабочие примеры использовали грубую силу, циклы или рекурсию для создания всех комбинаций наборов (см. Выше) в попытке проверить, существует ли уникальная комбинация. Это очень плохо масштабируется и с чем-то, кроме очень тривиального примера, не работает вообще в реальном мире. (Эта функция будет вызываться в режиме реального времени, когда товары добавляются в корзину, поэтому должна быть быстрой)

Многие исследования предполагают, что двустороннее сопоставление даст желаемый результат, но я могу только найти исследовательские статьи и довольно сложные математические тексты по этому вопросу. Какой-то псевдокод или базовая логика были бы великолепны.

---

Мои два вопроса в основном:

1) Кто-нибудь видит лучший / более быстрый / простой способ анализа потребительской корзины для получения соответствующих рекламных акций?
2) Предполагая, что я определил наиболее эффективный способ сопоставления товаров по соответствующим позициям, какой метод наименее дорогостоящий для определения списка товаров для розничной продажи по сравнению с рекламой.

Любая помощь будет принята с благодарностью, так как я больше не вижу света в конце туннеля! (Окончательное решение будет в.NET, и мы будем использовать SQL Server 2008 R2.)

Answer 1

Проверка каждой акции на действительность в данной корзине покупок может быть уменьшена до Max Flow. Описывая мое решение, я предполагаю, что вы можете реализовать и решить задачу о максимальном потоке на основе графов. Если нет, то это вторая проблема, которую нужно решить (и, к счастью, гораздо более общая).

Пусть вход для алгоритма будет следующим:

• Набор всех действительных предметов I, Не обязательно используется в окончательном кодировании алгоритма.
• Корзина для покупок C размера nподмножество I содержащие предметы C_1 ... C_n, таким образом C = {C_i}заi = 1...n
• Разовая акция P состоящий из m подмножества, каждое из которых содержит переменное количество элементов. Каждое подмножество S это подмножество I, Каждое подмножество не может иметь дубликатов, но один элемент может присутствовать в нескольких подмножествах.

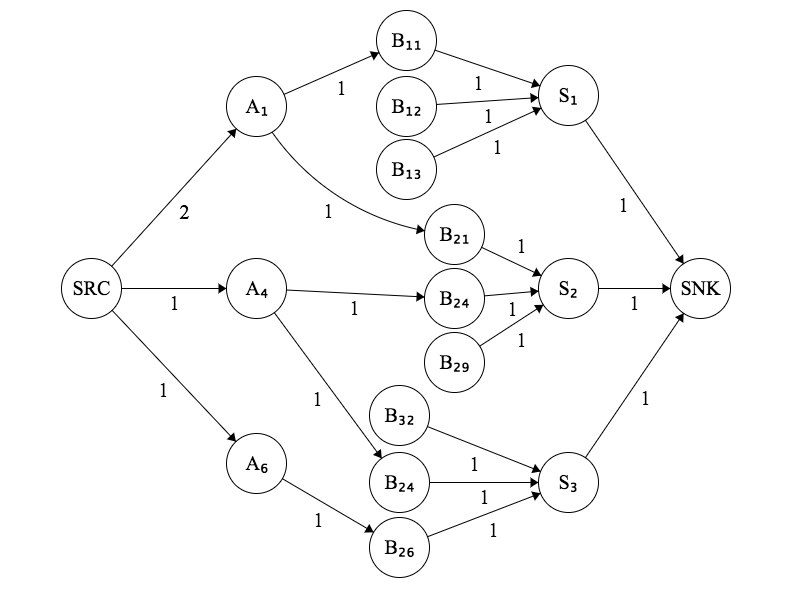
Построить график G следующее:

• Добавить супер исходный узел с меткой SOURCE
• Добавить узел супер-приемника, помеченный SINK
• За каждый уникальный предмет C_i в корзине C, добавьте доступный узел элемента A_iзатем добавьте ребро из SOURCE в A_i с емкостью, равной числу вхождений C_i в C,
• Для каждого подмножества S_i в продвижении Pдобавьте следующее:
  • Единый набор узлов S_iи край от S_i в SINK с мощностью 1,
  • Для каждого необходимого элемента I_j за S_i, обязательный элемент узла B_i_jи край от B_i_j в S_i с мощностью 1,
• Наконец, для каждой пары узлов A_x а также B_y таким образом, что предметы, которые они представляют, эквивалентны, край от A_x в B_y с мощностью 1,

Наконец, запустите алгоритм максимального потока с SOURCE в качестве источника и SINK как раковина. Если результирующий максимальный поток имеет значение, равное количеству подмножеств (m), затем выведите true - промоушен может быть удовлетворен этой корзиной покупок. В противном случае выведите false - промоушен не может быть удовлетворен этой корзиной покупок.

Например, для вашего заданного примера, с корзиной покупок {1,1,4,6}должен быть создан следующий график:

---

Ожидаемая сложность времени, где количество элементов nи количество подмножеств в продвижении m:

• Построение графика:
  • Добавление SOURCE а также SINK - O(1)
  • Добавление уникальных предметов из корзины и ребер из источника - O(N)
  • Добавление подмножеств и необходимых узлов элементов, а также ребер между - O(N*M)
  • Добавление ребер из узлов подмножества в сток - O(M)
  • Добавление ребер между соответствующими узлами элемента - O(N^2)
  • Всего - O(N^2 + N*M) = O(N * (N+M))
• Алгоритм максимального потока - см. Страницу википедии. Простая стоимость внедрения - O((N*M)^3), Может быть улучшен с помощью более сложного алгоритма.
• Получение решения - O(1),