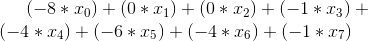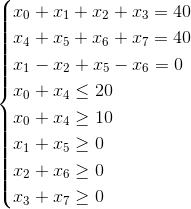Множитель нуля для значения в целевой функции не дает наиболее приемлемого решения
Я использую Pulp для решения линейной программы (также получаю тот же результат со Scipy). Так что что-то не так с моей линейной формулировкой программы, или я не знаю некоторых хитрых подробностей о том, как работает симплексный алгоритм.
Вот целевая функция для минимизации, обратите внимание, что множитель для x2 является 0так что я не ожидаю x1 или же x2 иметь какую-либо ценность, кроме 0, так как x3 не имеет максимального ограничения и -1 * x3 способен обеспечить большую ценность для минимизации:
Система линейных уравнений:
В качестве решения я получаю x2 = 20 даже если его множитель в целевой функции 0,
Если в целевой функции я поставил -2 * x3, тогда это работает просто отлично.
1 ответ
Решение, которое вы разместили, дает цель = -380. Проверьте x=[20,0,0,20,0,20,20,0]целевая функция также равна -380, что означает, что она также является оптимальной, поэтому у вас есть бесконечно много решений (легко показать, что любая выпуклая комбинация этих двух точек является оптимальной, см. любую книгу по линейному программированию). Проблема в том, что ваш решатель PuLP остановился, когда встретил одну оптимальную крайнюю точку. Если вы заинтересованы в получении всех оптимальных крайних точек, я бы порекомендовал вам использовать Cplex (это не бесплатно, но вы можете иметь право на академические инициативы IBM). Кроме того, вы можете установить метод решения Dual Simlex в своем решателе PuLP, чтобы заставить его двигаться в другом направлении, и есть вероятность, что вы получите другую крайнюю точку.