Подгонка распределения Вейбулла с использованием Scipy
Я пытаюсь воссоздать примерку распределения максимального правдоподобия, я уже могу сделать это в Matlab и R, но теперь я хочу использовать scipy. В частности, я хотел бы оценить параметры распределения Вейбулла для моего набора данных.
Я попробовал это:
import scipy.stats as s
import numpy as np
import matplotlib.pyplot as plt
def weib(x,n,a):
return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)
data = np.loadtxt("stack_data.csv")
(loc, scale) = s.exponweib.fit_loc_scale(data, 1, 1)
print loc, scale
x = np.linspace(data.min(), data.max(), 1000)
plt.plot(x, weib(x, loc, scale))
plt.hist(data, data.max(), normed=True)
plt.show()
И получите это:
(2.5827280639441961, 3.4955032285727947)
И дистрибутив, который выглядит так:
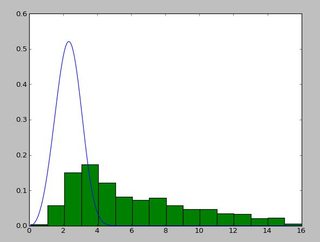
Я использовал exponweib после прочтения этого http://www.johndcook.com/distributions_scipy.html. Я также пробовал другие функции Вейбулла в scipy (на всякий случай!).
В Matlab (с использованием инструмента Distribution Fitting - см. Скриншот) и в R (с использованием функции библиотеки MASS fitdistr и пакет GAMLSS) я получаю параметры a (loc) и b (масштаб) больше как 1.58463497 5.93030013. Я считаю, что все три метода используют метод максимального правдоподобия для подгонки распределения.

Я разместил свои данные здесь, если вы хотите попробовать! И для полноты я использую Python 2.7.5, Scipy 0.12.0, R 2.15.2 и Matlab 2012b.
Почему я получаю другой результат!?
9 ответов
Я предполагаю, что вы хотите оценить параметр формы и масштаб распределения Вейбулла, сохраняя местоположение фиксированным. фиксация loc Предполагается, что значения ваших данных и распределения являются положительными с нижней границей на нуле.
floc=0 сохраняет местоположение на нулевом уровне, f0=1 сохраняет первый параметр формы экспоненциального вейбулла равным единице.
>>> stats.exponweib.fit(data, floc=0, f0=1)
[1, 1.8553346917584836, 0, 6.8820748596850905]
>>> stats.weibull_min.fit(data, floc=0)
[1.8553346917584836, 0, 6.8820748596850549]
Подгонка по сравнению с гистограммой выглядит хорошо, но не очень хорошо. Оценки параметров немного выше, чем те, что вы упоминаете, от R и Matlab.
Обновить
Самое близкое, что я могу получить к графику, который теперь доступен, с неограниченным подгонкой, но с использованием начальных значений. Сюжет еще менее острый. Значения примечания в подгонке, которые не имеют f перед, используются в качестве начальных значений.
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> plt.plot(data, stats.exponweib.pdf(data, *stats.exponweib.fit(data, 1, 1, scale=02, loc=0)))
>>> _ = plt.hist(data, bins=np.linspace(0, 16, 33), normed=True, alpha=0.5);
>>> plt.show()
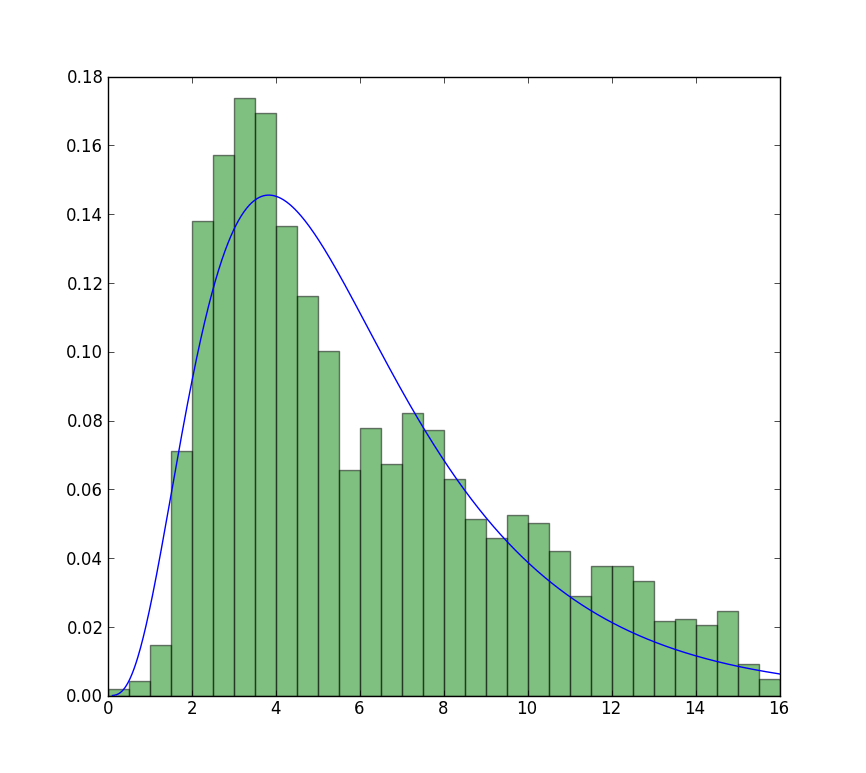
Легко проверить, какой результат является истинным MLE, просто нужна простая функция для вычисления вероятности записи:
>>> def wb2LL(p, x): #log-likelihood
return sum(log(stats.weibull_min.pdf(x, p[1], 0., p[0])))
>>> adata=loadtxt('/home/user/stack_data.csv')
>>> wb2LL(array([6.8820748596850905, 1.8553346917584836]), adata)
-8290.1227946678173
>>> wb2LL(array([5.93030013, 1.57463497]), adata)
-8410.3327470347667
Результат от fit метод exponweib и R fitdistr (@Warren) лучше и имеет более высокую вероятность регистрации. Скорее всего, это будет истинный MLE. Не удивительно, что результат от GAMLSS отличается. Это совершенно другая статистическая модель: Обобщенная аддитивная модель.
Все еще не убежден? Мы можем нарисовать двухмерный график доверительного интервала вокруг MLE, подробнее см. Книгу Микера и Эскобара). 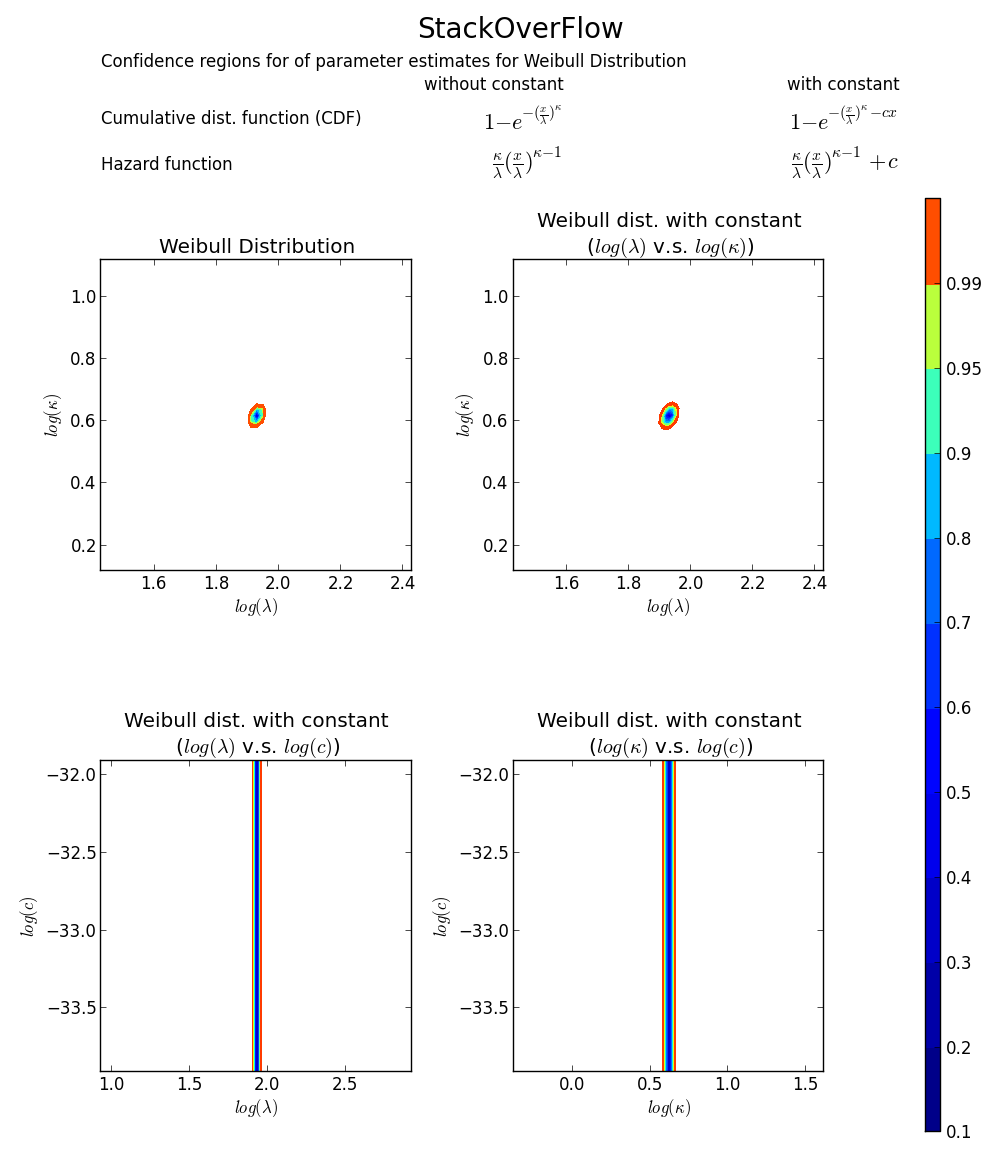
Опять же это подтверждает, что array([6.8820748596850905, 1.8553346917584836]) является правильным ответом, поскольку логарифмическая правдоподобность ниже, чем любая другая точка в пространстве параметров. Замечания:
>>> log(array([6.8820748596850905, 1.8553346917584836]))
array([ 1.92892018, 0.61806511])
BTW1, MLE fit может не соответствовать плотно распределенной гистограмме. Простой способ думать о MLE состоит в том, что MLE является оценкой параметра, наиболее вероятной с учетом наблюдаемых данных. Это не должно хорошо визуально соответствовать гистограмме, это будет что-то, что минимизирует среднеквадратичную ошибку.
Кстати, ваши данные выглядят как leptokurtic и искажены влево, что означает, что распределение Weibull может не соответствовать вашим данным. Попробуйте, например, Gompertz-Logistic, который повышает вероятность логарифмирования еще примерно на 100.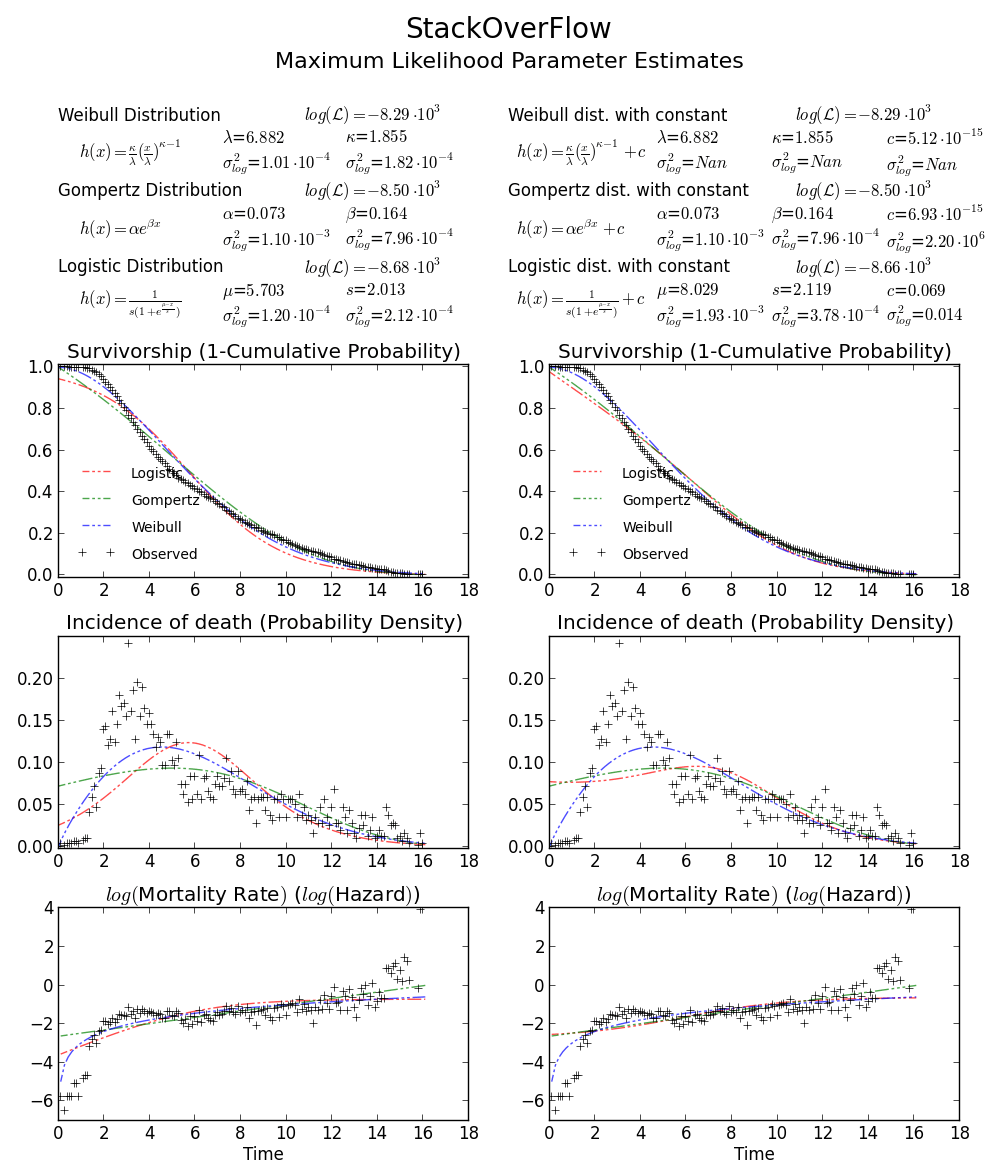
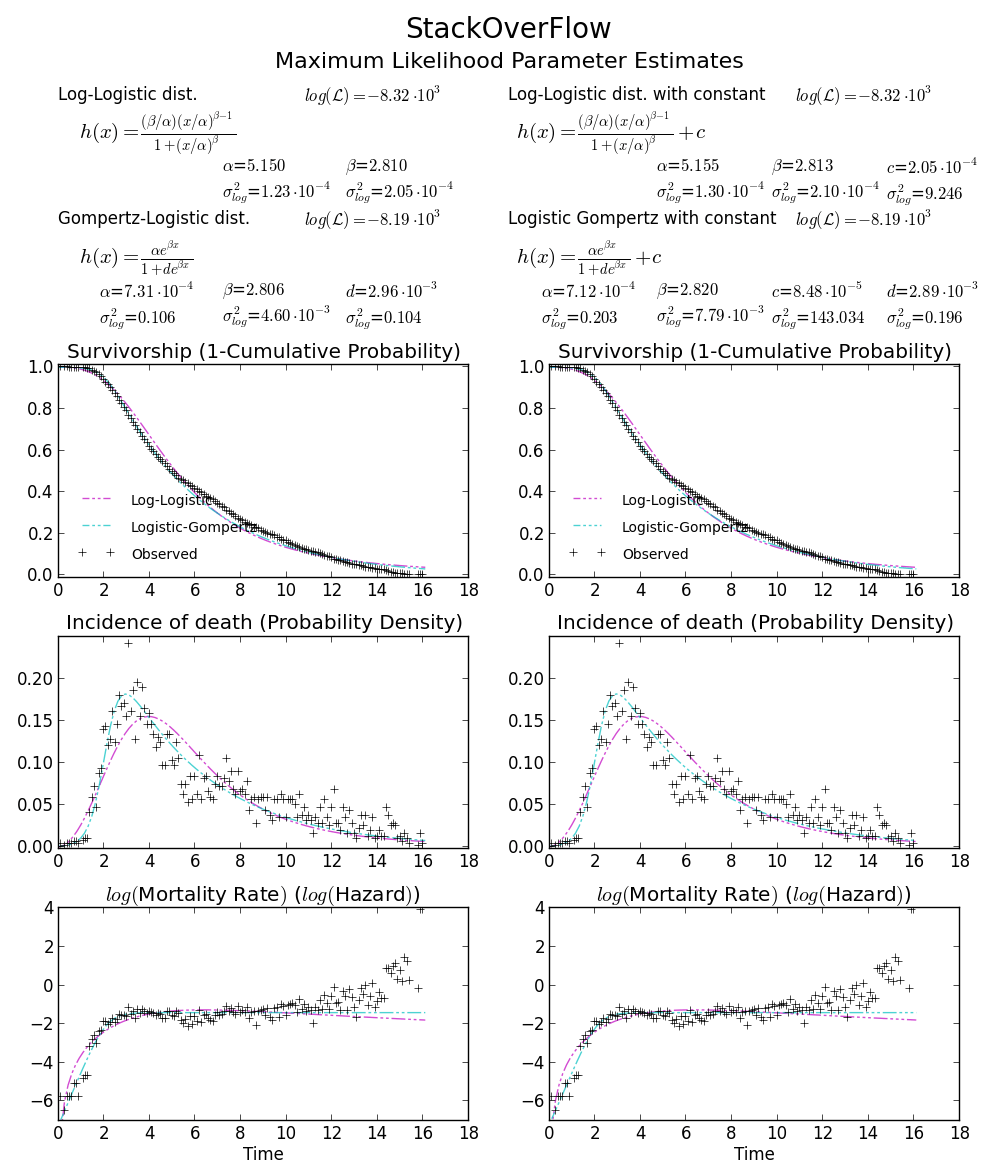 Ура!
Ура!
Я знаю, что это старый пост, но я столкнулся с подобной проблемой, и эта ветка помогла мне решить ее. Я подумал, что мое решение может быть полезным для таких, как я:
# Fit Weibull function, some explanation below
params = stats.exponweib.fit(data, floc=0, f0=1)
shape = params[1]
scale = params[3]
print 'shape:',shape
print 'scale:',scale
#### Plotting
# Histogram first
values,bins,hist = plt.hist(data,bins=51,range=(0,25),normed=True)
center = (bins[:-1] + bins[1:]) / 2.
# Using all params and the stats function
plt.plot(center,stats.exponweib.pdf(center,*params),lw=4,label='scipy')
# Using my own Weibull function as a check
def weibull(u,shape,scale):
'''Weibull distribution for wind speed u with shape parameter k and scale parameter A'''
return (shape / scale) * (u / scale)**(shape-1) * np.exp(-(u/scale)**shape)
plt.plot(center,weibull(center,shape,scale),label='Wind analysis',lw=2)
plt.legend()
Некоторая дополнительная информация, которая помогла мне понять:
Функция Scipy Weibull может принимать четыре входных параметра: (a,c),loc и scale. Вы хотите исправить loc и первый параметр формы (a), это делается с помощью floc=0,f0=1. Затем фитинг даст вам параметры c и масштаб, где c соответствует параметру формы двухпараметрического распределения Вейбулла (часто используется при анализе данных о ветре), а масштаб соответствует его масштабному коэффициенту.
Из документов:
exponweib.pdf(x, a, c) =
a * c * (1-exp(-x**c))**(a-1) * exp(-x**c)*x**(c-1)
Если а равен 1, то
exponweib.pdf(x, a, c) =
c * (1-exp(-x**c))**(0) * exp(-x**c)*x**(c-1)
= c * (1) * exp(-x**c)*x**(c-1)
= c * x **(c-1) * exp(-x**c)
Исходя из этого, связь с функцией Вейбулла "анализа ветра" должна быть более ясной.
Мне был любопытен ваш вопрос, и, несмотря на то, что это не ответ, он сравнивает Matlab результат с вашим результатом и с помощью результата leastsq, который показал наилучшую корреляцию с приведенными данными:
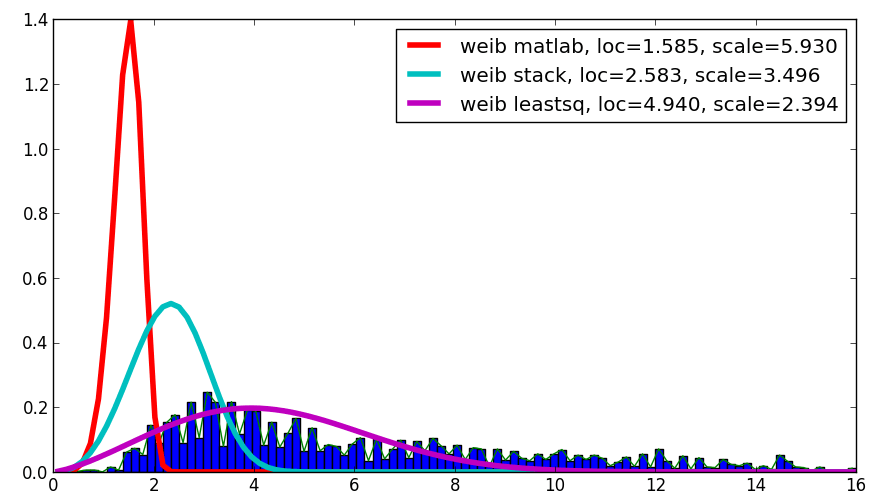
Код выглядит следующим образом:
import scipy.stats as s
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as mtrand
from scipy.integrate import quad
from scipy.optimize import leastsq
## my distribution (Inverse Normal with shape parameter mu=1.0)
def weib(x,n,a):
return (a / n) * (x / n)**(a-1) * np.exp(-(x/n)**a)
def residuals(p,x,y):
integral = quad( weib, 0, 16, args=(p[0],p[1]) )[0]
penalization = abs(1.-integral)*100000
return y - weib(x, p[0],p[1]) + penalization
#
data = np.loadtxt("stack_data.csv")
x = np.linspace(data.min(), data.max(), 100)
n, bins, patches = plt.hist(data,bins=x, normed=True)
binsm = (bins[1:]+bins[:-1])/2
popt, pcov = leastsq(func=residuals, x0=(1.,1.), args=(binsm,n))
loc, scale = 1.58463497, 5.93030013
plt.plot(binsm,n)
plt.plot(x, weib(x, loc, scale),
label='weib matlab, loc=%1.3f, scale=%1.3f' % (loc, scale), lw=4.)
loc, scale = s.exponweib.fit_loc_scale(data, 1, 1)
plt.plot(x, weib(x, loc, scale),
label='weib stack, loc=%1.3f, scale=%1.3f' % (loc, scale), lw=4.)
plt.plot(x, weib(x,*popt),
label='weib leastsq, loc=%1.3f, scale=%1.3f' % tuple(popt), lw=4.)
plt.legend(loc='upper right')
plt.show()
У меня была такая же проблема, но обнаружил, что настройка loc=0 в exponweib.fit заправил насос для оптимизации. Это было все, что было нужно из ответа@user333700. Я не могу загрузить ваши данные - ваша ссылка на данные указывает на изображение, а не на данные. Поэтому вместо этого я проверил свои данные:
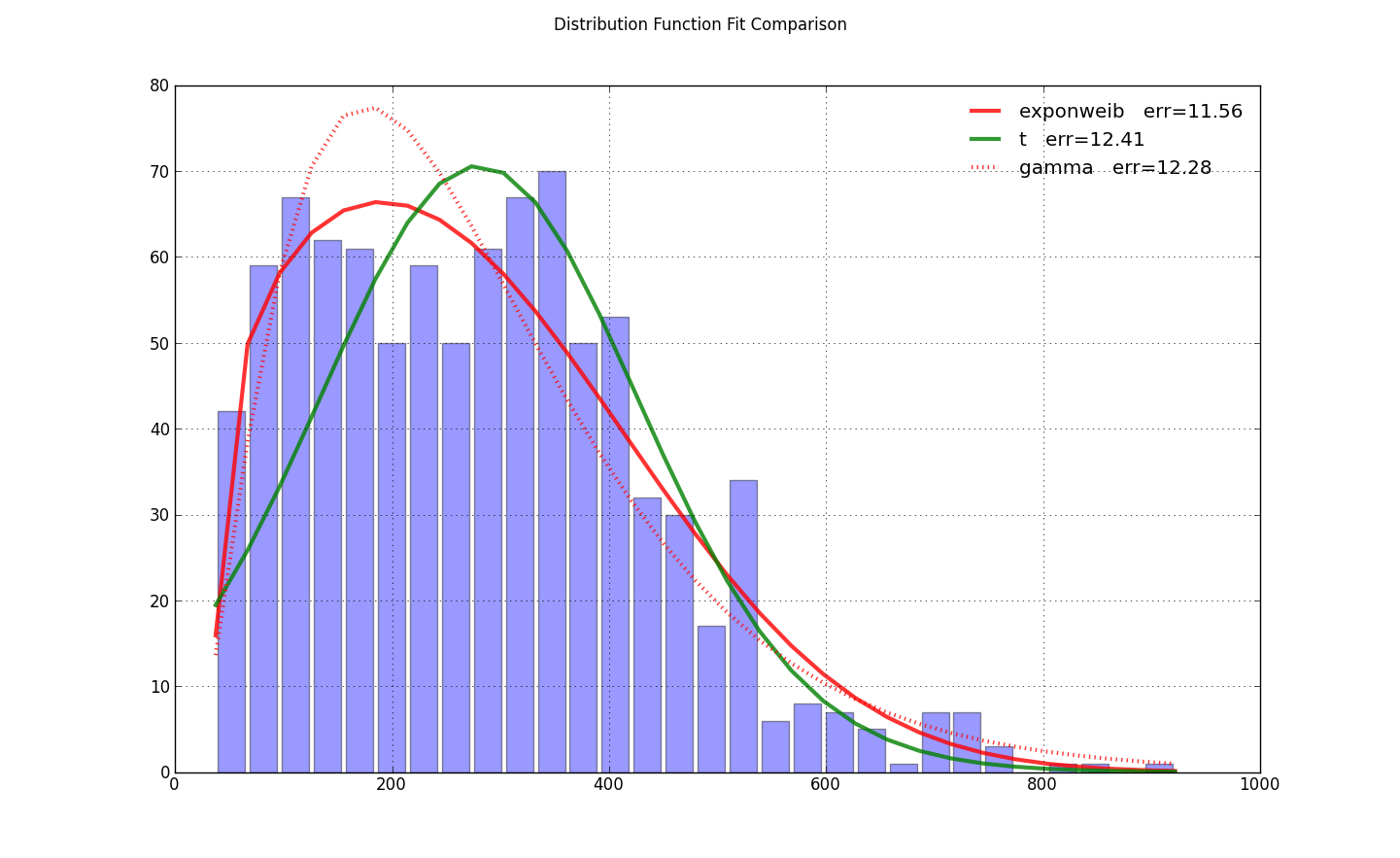
import scipy.stats as ss
import matplotlib.pyplot as plt
import numpy as np
N=30
counts, bins = np.histogram(x, bins=N)
bin_width = bins[1]-bins[0]
total_count = float(sum(counts))
f, ax = plt.subplots(1, 1)
f.suptitle(query_uri)
ax.bar(bins[:-1]+bin_width/2., counts, align='center', width=.85*bin_width)
ax.grid('on')
def fit_pdf(x, name='lognorm', color='r'):
dist = getattr(ss, name) # params = shape, loc, scale
# dist = ss.gamma # 3 params
params = dist.fit(x, loc=0) # 1-day lag minimum for shipping
y = dist.pdf(bins, *params)*total_count*bin_width
sqerror_sum = np.log(sum(ci*(yi - ci)**2. for (ci, yi) in zip(counts, y)))
ax.plot(bins, y, color, lw=3, alpha=0.6, label='%s err=%3.2f' % (name, sqerror_sum))
return y
colors = ['r-', 'g-', 'r:', 'g:']
for name, color in zip(['exponweib', 't', 'gamma'], colors): # 'lognorm', 'erlang', 'chi2', 'weibull_min',
y = fit_pdf(x, name=name, color=color)
ax.legend(loc='best', frameon=False)
plt.show()
Было несколько ответов на это уже здесь и в других местах. likt в распределении Вейбулла и данные на одном рисунке (с numpy и scipy)
Мне все еще потребовалось время, чтобы придумать чистый пример с игрушкой, поэтому я подумал, что было бы полезно опубликовать этот пост.
from scipy import stats
import matplotlib.pyplot as plt
#input for pseudo data
N = 10000
Kappa_in = 1.8
Lambda_in = 10
a_in = 1
loc_in = 0
#Generate data from given input
data = stats.exponweib.rvs(a=a_in,c=Kappa_in, loc=loc_in, scale=Lambda_in, size = N)
#The a and loc are fixed in the fit since it is standard to assume they are known
a_out, Kappa_out, loc_out, Lambda_out = stats.exponweib.fit(data, f0=a_in,floc=loc_in)
#Plot
bins = range(51)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(bins, stats.exponweib.pdf(bins, a=a_out,c=Kappa_out,loc=loc_out,scale = Lambda_out))
ax.hist(data, bins = bins , normed=True, alpha=0.5)
ax.annotate("Shape: $k = %.2f$ \n Scale: $\lambda = %.2f$"%(Kappa_out,Lambda_out), xy=(0.7, 0.85), xycoords=ax.transAxes)
plt.show()
Между тем, есть действительно хороший пакет: надежность. Вот документация: надежность @readthedocs.
Ваш код просто становится:
from reliability.Fitters import Fit_Weibull_2P
...
wb = Fit_Weibull_2P(failures=data)
plt.show()
Экономит много головной боли и делает красивые сюжеты.
Порядок loc и scale указывается в коде:
plt.plot(x, weib(x, scale, loc))
параметр масштаба должен стоять первым.
В функции подбора есть 3 параметра для рассмотрения:
Параметры формы: в этом случае у нас есть два параметра формы, которые можно фиксировать в соответствии с f0 и f1. (Попробуйте сами!). Обычно имя параметра обозначается через f%d, где d - номер фигуры.
Параметр location: Используйте floc, чтобы это исправить. Если вы не исправите floc, среднее значение данных будет выведено как loc.
Параметр масштаба: используйте fscale, чтобы исправить это.
Возврат любой посадки происходит в этом порядке.
Следуя принципу @Peter9192, я нашел наилучшее соответствие для CDF Вейбулла из ~20-30 выборок данных, используя следующее:_,gamma,_alpha=scipy.stats.exponweib.fit(data,floc=0,f0=1)
Формула для CDF:
1-np.exp(-np.power(x/alpha,gamma))
Значения для данных, которые я оценил, используя метод оценки КМ, соответствующий распределению Вейбулла, дали мне хорошие значения.
Чтобы исправить как 1, я не нашел loc=0, scale=1 как лучший метод, как вы можете ясно увидеть в 4 возвращаемых значениях параметров. Во-вторых, используя гамму, альфа из нее не выдает правильное среднее значение Вейбулла.
Наконец, я подтвердил, какой метод работает лучше всего, вычислив среднее значение распределения Вейбулла, используя:Mean=alpha*scipy.special.gamma(1+(1/gamma))Значения, которые я получил, соответствовали моему заявлению.
Вы можете проверить средние значения и формулы CDF здесь для справки: https://en.m.wikipedia.org/wiki/Weibull_distribution