Факториальная петля становится 0
Я запустил простую программу на скомпилированном языке, которая вычисляет факториал первых нескольких натуральных чисел, используя два простых цикла, внешний для отслеживания которых является числом, которое мы вычисляем, и внутренний для вычисления факториала умножение каждого натурального числа от 1 до самого числа. Программа отлично работает для первых натуральных чисел, а затем, начиная примерно с 13-го значения, вычисленные факториалы явно неверны. Это связано с целочисленной арифметикой, реализованной в современном компьютере, и я могу понять, почему могут возникать отрицательные значения. Однако я не понимаю, почему, и это то, что я тестировал на разных компьютерах, после очень небольшого количества факторных вычислений оно всегда достигает нуля. Конечно, если n-й факториал оценивается как 0, также (n+1)-й факториал будет оцениваться как 0 и т. Д., Но почему число 0 всегда происходит после очень небольшого числа факторные расчеты?
РЕДАКТИРОВАТЬ: Вы можете спросить, почему я использовал два разных цикла вместо одного... Я сделал это, чтобы заставить компьютер пересчитать каждый факториал с самого начала, просто чтобы проверить, что на самом деле факториал становится всегда 0, и это не случайно.
Вот мой вывод:
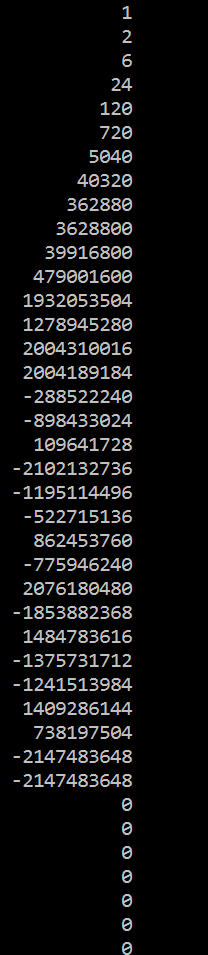
2 ответа
Начиная с 34!, все факториалы делятся на 2^32. Поэтому, когда ваша компьютерная программа вычисляет результаты по модулю 2^32 (что, хотя вы не говорите, какой язык программирования вы используете, это вероятно), тогда результаты всегда равны 0.
Вот программа, которая вычисляет факториалы мод 2 ^ 32 в Python:
def sint(r):
r %= (1 << 32)
return r if r < (1 << 31) else r - (1 << 32)
r = 1
for i in xrange(1, 40):
r *= i
print '%d! = %d mod 2^32' % (i, sint(r))
Что дает этот вывод, который согласуется с выводом вашей собственной программы:
1! = 1 mod 2^32
2! = 2 mod 2^32
3! = 6 mod 2^32
4! = 24 mod 2^32
5! = 120 mod 2^32
6! = 720 mod 2^32
7! = 5040 mod 2^32
8! = 40320 mod 2^32
9! = 362880 mod 2^32
10! = 3628800 mod 2^32
11! = 39916800 mod 2^32
12! = 479001600 mod 2^32
13! = 1932053504 mod 2^32
14! = 1278945280 mod 2^32
15! = 2004310016 mod 2^32
16! = 2004189184 mod 2^32
17! = -288522240 mod 2^32
18! = -898433024 mod 2^32
19! = 109641728 mod 2^32
20! = -2102132736 mod 2^32
21! = -1195114496 mod 2^32
22! = -522715136 mod 2^32
23! = 862453760 mod 2^32
24! = -775946240 mod 2^32
25! = 2076180480 mod 2^32
26! = -1853882368 mod 2^32
27! = 1484783616 mod 2^32
28! = -1375731712 mod 2^32
29! = -1241513984 mod 2^32
30! = 1409286144 mod 2^32
31! = 738197504 mod 2^32
32! = -2147483648 mod 2^32
33! = -2147483648 mod 2^32
34! = 0 mod 2^32
35! = 0 mod 2^32
36! = 0 mod 2^32
37! = 0 mod 2^32
38! = 0 mod 2^32
39! = 0 mod 2^32
И вот таблица точных значений этого диапазона факториалов, показывающая, сколько степеней 2 содержит каждая:
1! = 1. Divisible by 2^0
2! = 2. Divisible by 2^1
3! = 6. Divisible by 2^1
4! = 24. Divisible by 2^3
5! = 120. Divisible by 2^3
6! = 720. Divisible by 2^4
7! = 5040. Divisible by 2^4
8! = 40320. Divisible by 2^7
9! = 362880. Divisible by 2^7
10! = 3628800. Divisible by 2^8
11! = 39916800. Divisible by 2^8
12! = 479001600. Divisible by 2^10
13! = 6227020800. Divisible by 2^10
14! = 87178291200. Divisible by 2^11
15! = 1307674368000. Divisible by 2^11
16! = 20922789888000. Divisible by 2^15
17! = 355687428096000. Divisible by 2^15
18! = 6402373705728000. Divisible by 2^16
19! = 121645100408832000. Divisible by 2^16
20! = 2432902008176640000. Divisible by 2^18
21! = 51090942171709440000. Divisible by 2^18
22! = 1124000727777607680000. Divisible by 2^19
23! = 25852016738884976640000. Divisible by 2^19
24! = 620448401733239439360000. Divisible by 2^22
25! = 15511210043330985984000000. Divisible by 2^22
26! = 403291461126605635584000000. Divisible by 2^23
27! = 10888869450418352160768000000. Divisible by 2^23
28! = 304888344611713860501504000000. Divisible by 2^25
29! = 8841761993739701954543616000000. Divisible by 2^25
30! = 265252859812191058636308480000000. Divisible by 2^26
31! = 8222838654177922817725562880000000. Divisible by 2^26
32! = 263130836933693530167218012160000000. Divisible by 2^31
33! = 8683317618811886495518194401280000000. Divisible by 2^31
34! = 295232799039604140847618609643520000000. Divisible by 2^32
35! = 10333147966386144929666651337523200000000. Divisible by 2^32
36! = 371993326789901217467999448150835200000000. Divisible by 2^34
37! = 13763753091226345046315979581580902400000000. Divisible by 2^34
38! = 523022617466601111760007224100074291200000000. Divisible by 2^35
39! = 20397882081197443358640281739902897356800000000. Divisible by 2^35
Каждое умножение добавляет ноль битов справа, пока на некоторой итерации самые левые биты не будут отброшены из-за переполнения. Эффект в действии:
int i, x=1;
for (i=1; i <=50; i++) {
x *= i;
for (int i = 31; i >= 0; --i) {
printf("%i",(x >> i) & 1);
}
printf("\n");
}
Выходные биты:
0000000000000000000000000000000100000000000000000000000000000010 00000000000000000000000000000110 00000000000000000000000000011000 00000000000000000000000001111000 00000000000000000000001011010000 00000000000000000001001110110000 00000000000000001001110110000000 00000000000001011000100110000000 00000000001101110101111100000000 00000010011000010001010100000000 00011100100011001111110000000000 01110011001010001100110000000000 01001100001110110010100000000000 01110111011101110101100000000000 011101110111010110000000000000001110111011001101100000000000000011001010011100110000000000000000 00000110100010010000000000000000100000101011010000000000000000001011100011000100000000000000000011100000110110000000000000000000 001100111000000000000000000000001101000000000000000000000000000010000000000000000000000000000000 00000000000000000000000000000000
Обратите внимание, что прежде чем мы получим ноль - мы получим INT_MIN. Добавление еще одного нулевого бита - отбрасывает знаковый бит и, таким образом, из INT_MIN мы получаем обычный ноль.