2 выполнимости сильно связанного компонента топологического упорядочения

Question

Я решаю проблему с двумя выполнимостями с SCC, и у меня есть вопрос о топологической сортировке. Алгоритм, на котором я это основываю, заключается в обработке SCC в обратном топологическом порядке, что хорошо, когда все они подключены. Мой алгоритм ломается в таких случаях:

3 3
-2 3
1 -2
-2 -1

Это делает график, который выглядит следующим образом: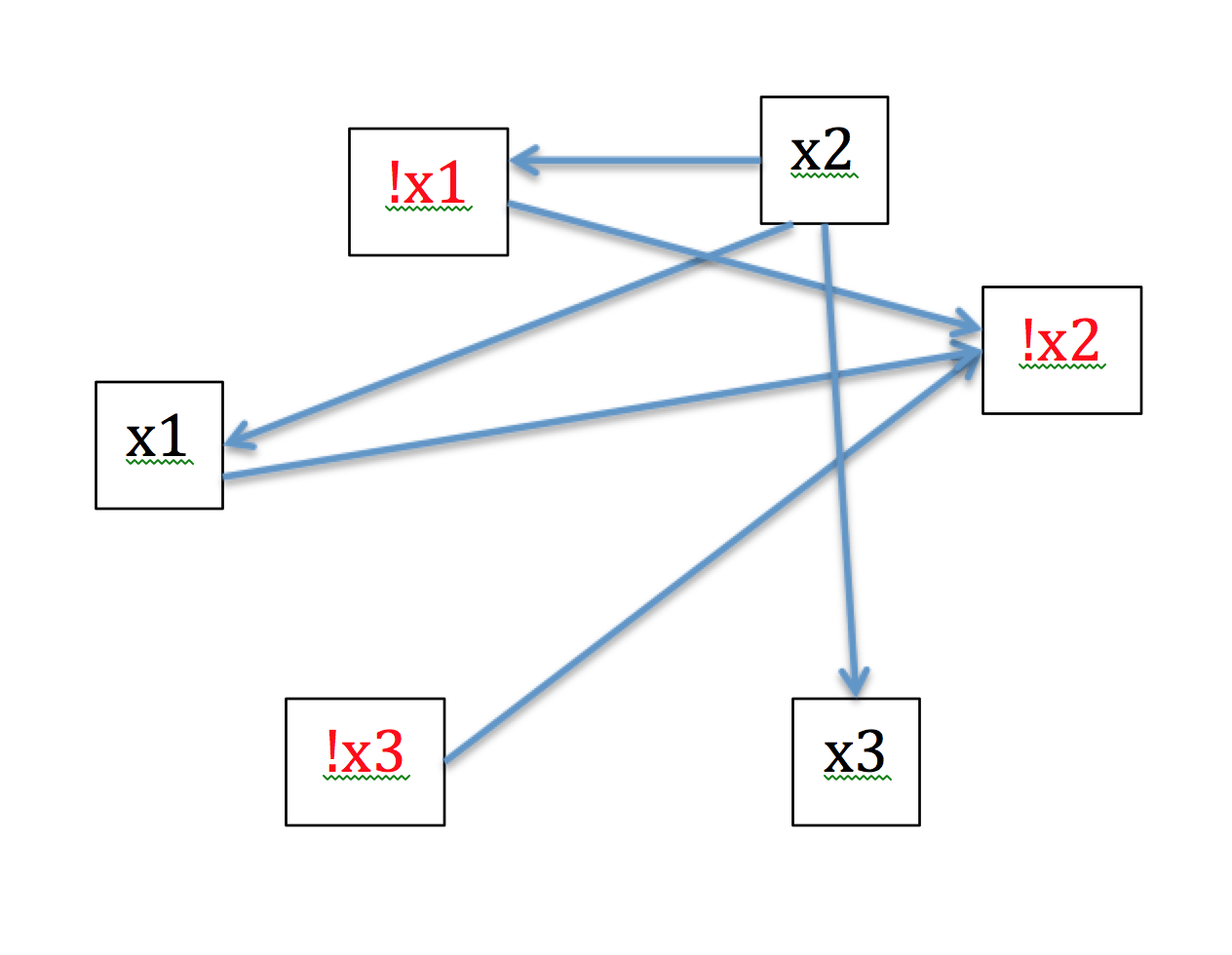

На этом графике есть два источника и два приемника, и в зависимости от того, с чего вы начинаете, существует несколько топологических сортировок, поэтому есть два возможных конечных узла. Циклов нет, поэтому каждый узел является SCC. Существует несколько путей от источника до приемника, поэтому, когда я делаю обратный топологический порядок, я могу либо начать с приемника х3, либо приемника! Х2. Путь, который даст мне правильный ответ, должен начинаться с! X2, что приведет к 1, -2, -3 или -1, -2, -3, оба из которых являются решениями. Но если я начну с x3, один из возможных результатов - это -1, 2, 3, что не является решением.

Итак, когда я смотрю на мои две раковины, как я могу решить топологически, какая из них последняя? Ясно, что ответ! X2, но я пытаюсь выяснить, как алгоритм это определит. Я вижу четыре возможных идеи:

• !x2 последний, потому что он имеет больше узлов, ведущих в него
• !x2 последний, потому что он находится в конце более длинного пути
• Установите значение истинности каждого из приемников, прежде чем я начну что-либо обрабатывать
• Нет способа узнать, какой из них последний, поэтому создайте все возможные решения и протестируйте каждое из них, чтобы увидеть, работает ли оно.

Или есть что-то в топологическом заказе SCC, которых я здесь не получу? Это основано на алгоритме, который я использовал для прохождения назначения Сильно связанных компонентов в более раннем курсе, поэтому он не может быть полностью ошибочным.

Answer 1

Не видя ваш код, я не могу быть уверен, но я предполагаю, что когда вы обрабатываете литералы, вы устанавливаете значение, а затем переворачиваете его позже, когда сталкиваетесь с его отрицанием глубже в топологическом порядке. Ключевым моментом является то, что как только вы установите переменную, вы больше не будете ее менять. Пропустить литерал любой переменной, которая уже имеет заданное значение.

Отредактировано, чтобы добавить: Из вашего комментария я думаю, что вижу проблему. Вы упоминаете установку переменной x2 в true, когда! X2 стоит первым в обратном топологическом порядке. Вы должны установить литерал! X2 в true, что означает, что вы устанавливаете переменную x2 в false. Если вы сделаете это, то ваш решатель должен работать независимо от того, с какого из приемников вы начинаете.