Обход бинарного дерева для получения условий расщепления - ctree(party), рекурсивная функция

Question

Я пытаюсь воспроизвести ошибку, полученную с моим набором данных, используя общий набор данных. Пожалуйста, поправьте меня, если я что-то упустил.

После примерки Classification использование дерева library(party)Я пытаюсь получить условия разделения дерева на каждом узле. Мне удалось написать код, который, по моему мнению, работал нормально, пока я не нашел ошибку. Может ли кто-нибудь помочь мне решить это?

Мой код:

 require(party)
 iris$Petal.Width <- as.factor(iris$Petal.Width)#imp to convert to factorial
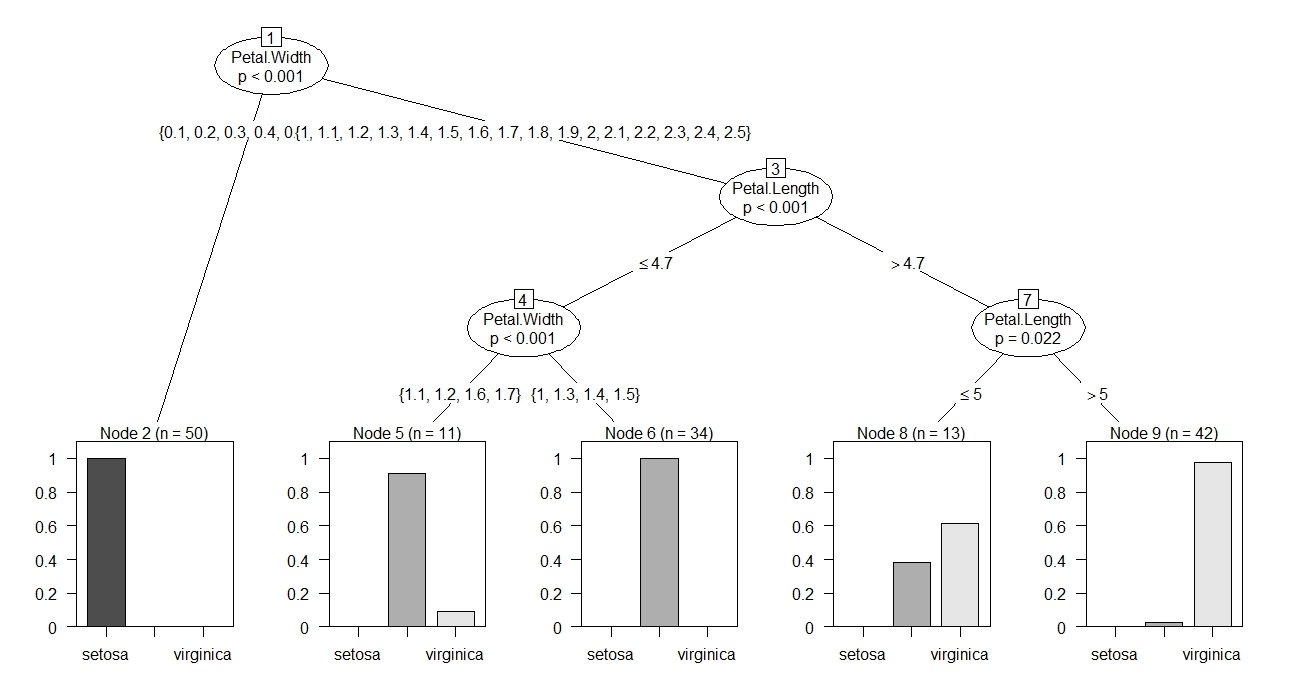
 (ct <- ctree(Species ~ ., data = iris))
 plot(ct)
 #print(ct)
  a <- ct #convert it to s4 object
  t <- a@tree

 #recursive function to traverse the tree and get the splitting conditions

 recurse_tree <- function(tree,ret_list=list(),sub_list=list()){
   if(!tree$terminal){
     sub_list$assign <-list(tree$psplit$splitpoint,tree$psplit$variableName,class(tree$psplit))
     names(sub_list)[which(names(sub_list)=="assign")] <- paste("node",tree$nodeID,sep="")
     ret_list <- recurse_tree(tree$left, ret_list, sub_list)
     ret_list <- recurse_tree(tree$right, ret_list, sub_list)

  }
  if(tree$terminal){
    ret_list$assign <- c(sub_list, tree$prediction)
    names(ret_list)[which(names(ret_list)=="assign")] <- paste("node",tree$nodeID,sep="")
    return(ret_list)
   }
   return(ret_list)
  }

  result <- recurse_tree(t) #call to the functions

Теперь результат дает мне список всех узлов и условий разделения и прогнозов (я предположил). Но когда я проверяю условия разделения для

• ожидаемый результат на Node5: {1.1, 1.2, 1.6, 1.7} # from printing the tree print(ct), I get this

• вывод, который я получаю на Node5 из своей функции: {"1", "1.3","1.4","1.5" }, что в основном является условием разделения Node6, что неверно. Как я это получил?

  z <- result[2] #I know node5 is second in the list

  z <- unlist(z,recursive = F,use.names = T) #unlist
  levels(z[[3]][[1]]) [which((z[[3]][[1]])==0)] #to find levels of corresponding values
  

В чем я сомневаюсь, моя функция (recurse_tree) всегда дает мне условия разделения правого конечного узла, а не левого узла. Любая помощь будет оценена.