Оптимизация для глобального минимума

Question

Я пытаюсь использовать optimize() найти минимальное значение n для следующей функции (нижняя граница Клоппера-Пирсона):

f <- function (n, p=0.5) 
 (1 + (n - p*n + 1) / 
    (p*n*qf(p= .025, df1= 2*p, df2= 2*(n - p + 1))))^-1

И вот как я попытался его оптимизировать:

n_clop <- optimize(f.1, c(300,400), maximum = FALSE, p=0.5)
n_clop

Я делал это в течение интервала [300 400], потому что подозреваю, что значение находится между ними, но в конечном итоге я хотел бы провести оптимизацию между 0 и бесконечностью. Кажется, что эта команда производит локальный минимум, потому что независимо от интервала она создает нижнюю границу этого интервала как минимум - что я не подозреваю у Клоппера-Пирсона. Итак, два моих вопроса: как правильно найти глобальный минимум в R и как сделать это за любой интервал?

Answer 1

Я очень кратко просмотрел страницу Википедии, на которую вы ссылались, и не вижу никаких явных опечаток в вашей формуле (хотя мне кажется, что это должно быть 0,975=1-альфа /2, а не 0,025= альфа /2?). Тем не менее, оценка функции, которую вы закодировали в очень широком масштабе, показывает, что нет никаких локальных минимумов, которые могли бы вас испортить. Мое сильное предположение состоит в том, что либо ваша логика неверна (т. Е. N->0 - это действительно правильный ответ), либо вы не закодировали то, что, по вашему мнению, кодируете, из-за опечатки (возможно, в статье Википедии, хотя это кажется маловероятным) или Thinko.

f <- function (n, p=0.5) 
 (1 + (n - p*n + 1) / 
    (p*n*qf(p= .025, df1= 2*p, df2= 2*(n - p + 1))))^-1

Убедитесь, что вы получаете правильный ответ для выбранного интервала:

curve(f(x),c(300,400)) 

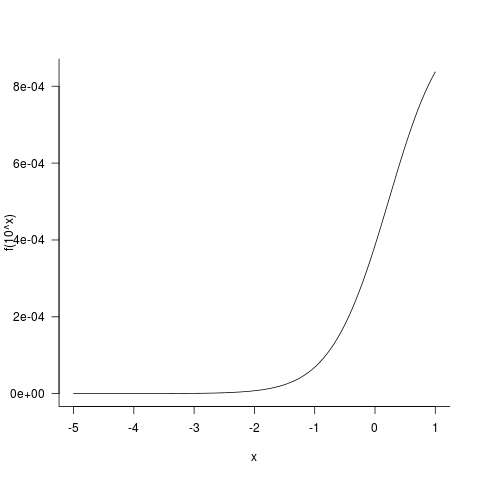
Оценка в широком диапазоне (n= от 0,00001 до 1000000):

curve(f(10^x),c(-5,7))

Как говорит @MrFlick, глобальная оптимизация трудна. Вы могли бы начать с optim(...method="SANN") но лучший ответ определенно зависит от конкретного случая.