Как подобрать отрезки, которые находятся внутри или пересекаются по кругу?
У меня есть наборы отрезков AB1, AB2, ... ABn, У каждого есть (Ax, Ay), (Bx, By) координаты. Тогда у меня есть круг с координатами центра (Cx, Cy) и r (радиус).
Проблема: Как я могу определить, какой отрезок линии лежит на окружности (на рисунке) ИЛИ нет? 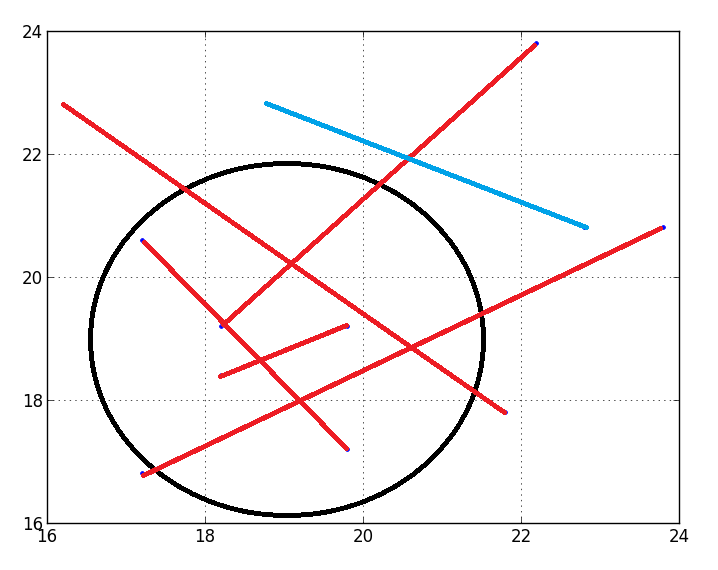 ,
,
Я попытался сформулировать свою идею на Python:
import numpy as np
import pylab as plt
def detect(A,B, C, r):
'''
Returns 'True' if line is inside or intersected the circle, otherwise 'False'.
Inputs:
- A - segment line coordinate (Ax, Ay)
- B - segment line coordinate (Bx, By)
- C - circle coordinate (Cx, Cy)
- r - circle radius
'''
# Do process for detection
return (boolean)
def plot_detected(An, Bn, C, r):
'''
Plots newly detected line segments with red color
while the rest remains with blue color
'''
plt.figure(1)
plt.subplot(111)
for A, B in zip(An, Bn):
if detect(A, B, C, r):
line1, = plt.plot([ A[0], B[0] ], [ A[1], B[1] ], 'ro-')
else:
line2, = plt.plot([ A[0], B[0] ], [ A[1], B[1] ], 'bo-')
pl.legend([line1, line2], ('detected','un-detected'))
plt.show()
def main():
C = [18.5, 18.5]
r = 2.4
Ax = np.array([16.2, 17.2, 22.2, 18.2, 23.8, 18.8])
Ay = np.array([22.8, 20.6, 23.8, 18.4, 20.8, 22.8])
Bx = np.array([21.8, 19.8, 18.2, 19.8, 17.2, 22.8])
By = np.array([17.8, 17.2, 19.2, 19.2, 16.8, 20.8])
An = np.vstack([Ax, Ay]).T
Bn = np.vstack([Bx, By]).T
plot_detected(An, Bn, C, r)
if __name__ == '__main__':
main()
Спасибо за вашу помощь заранее.
2 ответа
Для каждой линии вы должны быть в состоянии вычислить точку на линии, которая минимально удалена от центра круга. Для этого вы проецируете вектор положения центра на вектор направления линии. Назовите эту минимально удаленную точку P. Если P находится внутри окружности (т. Е. Площадь суммы квадратов ее координат меньше радиуса окружности), а P также находится между конечными точками отрезка, то отрезок линии пересекает круг.
Вы также должны проверить, находятся ли сами конечные точки линии внутри круга.
def detect( A, B, C, r ):
# First, let's express each vector as a complex number.
# This simplifies the rest of the code because we can then subtract them
# from each other in one statement, or find their length with one statement.
# (Downside: it does not allow us to generalize the code to spheres in 3D.)
OA = complex( *A )
OB = complex( *B )
OC = complex( *C )
# Now let's translate into a coordinate system where A is the origin
AB = OB - OA
AC = OC - OA
# Before we go further let's cover one special case: if either A or B is actually in
# the circle, then mark it as a detection
BC = OC - OB
if abs( BC ) < r or abs( AC ) < r: return True
# Project C onto the line to find P, the point on the line that is closest to the circle centre
AB_normalized = AB / abs( AB )
AP_distance = AC.real * AB_normalized.real + AC.imag * AB_normalized.imag # dot product (scalar result)
AP = AP_distance * AB_normalized # actual position of P relative to A (vector result)
# If AB intersects the circle, and neither A nor B itself is in the circle,
# then P, the point on the extended line that is closest to the circle centre, must be...
# (1) ...within the segment AB:
AP_proportion = AP_distance / abs( AB ) # scalar value: how far along AB is P?
in_segment = 0 <= AP_proportion <= 1
# ...and (2) within the circle:
CP = AP - AC
in_circle = abs( CP ) < r
detected = in_circle and in_segment
#OP = OA + AP
#plt.plot( [OC.real, OP.real], [OC.imag, OP.imag], {True:'rs--', False:'bs--'}[detected] )
return detected
def plot_detected(An, Bn, C, r):
'''
Plots newly detected line segments with red color
while the rest remains with blue color
'''
plt.figure(1)
plt.clf()
plt.subplot(111)
for A, B in zip(An, Bn):
if detect(A, B, C, r):
line1, = plt.plot([ A[0], B[0] ], [ A[1], B[1] ], 'ro-')
else:
line2, = plt.plot([ A[0], B[0] ], [ A[1], B[1] ], 'bo-')
plt.legend([line1, line2], ('detected','un-detected'))
circle = mpatches.Circle( C, r, fc="none", ec='k' )
plt.gca().add_patch(circle)
plt.gca().set_aspect('equal')
1-й: устранение неоднозначности топологии определения задачи
Определение терминов:
Все "отрезки" даны.
Каждый отрезок определяется декартовой парой
[x,y]для каждой из его конечных точек.
Изначальное утверждение вопроса о топологическом состоянии гласит:
определить, какой отрезок линии лежит на окружности (на рисунке) ИЛИ нет?
Авторский комментарий добавляет:
найдите, какие отрезки не только пересекаются, но и лежат в круге.
Название вопроса гласит:
подобрать отрезки, которые находятся внутри или пересекают окружность
Из заголовка и подтверждения комментария кажется, что для соответствия топологическому условию " отрезка " " лежать на окружности" достаточно, если какая-либо из его конечных точек { 1 | 2 } находится внутри круга.
Если это топологическое допущение не сработает, правильное решение с векторно-нормальным расстоянием не будет.
Решение:
на основе однозначного определения терминологии и условия топологии набор " отрезка ", соответствующих определенным ограничениям, получается путем:
def detect( A, B, C, r ):
'''
Returns 'True' if line is inside or intersected the circle, otherwise 'False'.
Inputs:
- A - segment line coordinate (Ax, Ay)
- B - segment line coordinate (Bx, By)
- C - circle coordinate (Cx, Cy)
- r - circle radius
'''
# Do process for detection
aBooleanANSWER = ( aCartesianDISTANCE( A, C ) <= r )
or
( aCartesianDISTANCE( B, C ) <= r )
return ( aBooleanANSWER )