Поиск и вставка недвоичного дерева
Я искал немного, но не нашел ответа на этот вопрос..
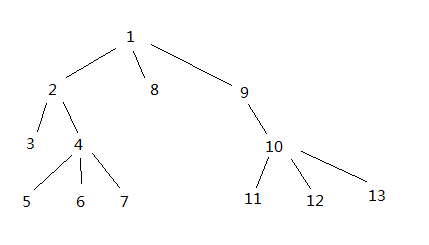
Я построил недвоичное дерево, поэтому каждый узел может иметь любое количество дочерних элементов (я думаю, это называется n-арным деревом)
Чтобы помочь с поиском, я дал каждому узлу номер при построении дерева, чтобы дочерние узлы каждого узла были больше, а также все узлы справа от него.
что-то вроде этого:
Таким образом, я получаю время входа в систему для поиска
Проблема возникает, когда я хочу вставить узлы. Эта модель не будет работать, если я хочу вставить узлы в любом месте, кроме конца.
Я думал о нескольких способах сделать это,
вставьте новые узлы в нужное место, затем обновите количество всех узлов "позади" него.
вместо использования одного числа для представления каждого узла используйте массив чисел. Числа в массиве будут представлять его местоположение на этом конкретном уровне. Например, узел 1 будет {0}. Узел 9 будет {0,2}. Узел 7 будет {0, 0, 1, 2}. Теперь при вставке мне просто нужно изменить цифры на этом уровне.
забудьте всю нумерацию и просто сравнивайте каждый узел, пока не найдете правильный. Для вставки не нужно заботиться о цифрах.
У меня вопрос, какой путь будет лучше? Я не уверен, что использование массива целых чисел для представления каждого узла очень быстро.. может быть, оно все же быстрее, чем первый способ? Есть ли другие способы сделать это?
Заранее спасибо.
1 ответ
Я понимаю, что ваша проблема состоит в том, чтобы назначить уникальный идентификатор каждому узлу таким образом, чтобы вы могли найти узел с заданным уникальным идентификатором в сублинейное время.
Обычно это не проблема для временных (в памяти) структур данных, потому что типичные реализации дерева никогда не перемещают узел в памяти (до тех пор, пока он не будет удален). Это позволяет использовать адрес узла в качестве уникального идентификатора, который обеспечивает доступ O(1). Языки, отличные от C, наряжают это в объект, такой как итератор дерева или ссылка на узел, но принцип скрыт.
Однако бывают случаи, когда вам действительно необходимо иметь возможность прикрепить фиксированный на все время идентификатор к узлу дерева таким образом, чтобы он был устойчивым, например, для сохранения дерева в постоянном хранилище, а затем повторной его инициализации. в другом исполняемом образе.
Один известный хак - использовать идентификаторы с плавающей точкой. Когда новый узел вставлен, его идентификатор назначается как среднее значение его непосредственных соседей. В целях этого вычисления мы притворяемся, что слева от дерева есть узел с идентификатором 0.0 и узел справа с идентификатором 1.0, поэтому у каждого узла есть два соседа, даже если это новый левый или правый самый узел. В частности, корневому узлу присваивается идентификатор 0,5, который является средним значением 0,0 и 1,0 мнимых граничных узлов.
К сожалению, точность с плавающей точкой не бесконечна, и этот хак работает лучше всего, если вставки всегда находятся в случайных местах дерева. Если вы вставите все узлы в конце, вы быстро исчерпаете точность с плавающей запятой. Вы могли бы периодически перенумеровать все узлы, но это противоречит цели иметь постоянный неизменяемый уникальный идентификатор узла. (Однако для некоторых проблемных доменов это приемлемо.)
Конечно, вам не обязательно использовать плавающую точку. Двойная стандартная архитектура имеет 53 бита точности, что достаточно, если ваши вставки стохастические, и очень мало, если вы всегда вставляете в одном и том же месте; Вы можете использовать все 64 бита 64-битного целого без знака, (концептуально) найдя фиксированную двоичную точку до старшего бита. Среднее вычисление работает так же, за исключением того, что вам нужно в особом случае вычисление со значением 1,0.
По сути, это то же самое, что ваша идея пометить узлы вектором индексов. Преимущество этой схемы в том, что она никогда не иссякает, и недостаток в том, что векторы могут быть довольно длинными. Вы также можете использовать гибридное решение, в котором вы начинаете новый уровень, только когда у вас заканчивается точность с текущим уровнем.