Сокращение сети сортировки

Question

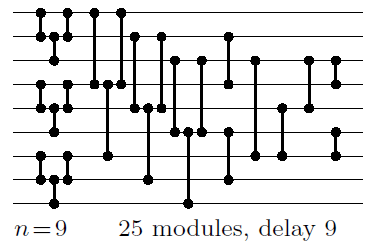
Сортировочная сеть - это компоновка из 2 входных компараторов, которые могут сортировать входную последовательность из n элементов. Например, вот сортировочная сеть для 9 элементов ввода:

Каждая из вертикальных линий представляет собой 2 входных компаратора, входная последовательность вводится слева, а отсортированная последовательность отображается справа.

Мой вопрос: как доказать, что если мы удалим верхнюю или нижнюю строку любой действительной n-входной сети сортировки, мы получим действительную сортировочную сеть для (n-1) входов? Как насчет удаления любой из средних линий?

У меня есть ощущение, что это можно показать с помощью графического представления сортировочной сети, но я не могу найти подходящее представление.

Answer 1

Верхняя или нижняя строка действительно может быть удалена. Одним из способов доказать это является использование принципа Кнута 0-1, который гласит, что сеть сортировки правильна тогда и только тогда, когда каждая последовательность нулей и единиц отсортирована правильно. Позволять S быть сортировочной сетью и пусть S' быть S со снятой верхней строкой. Позволять x быть 0-1 входом в S', Проходить 0x в S, По индукции мы можем показать, что значения после k этапы согласуются (за исключением удаленной верхней линии), так как все ворота, включающие верхнюю линию, не используются. Это следует из того S' это правильная сортировочная сеть.

В общем, мы не можем удалить среднюю линию. Рассмотрим, например, сеть

1 *   *
  |   |
2 * * *
    |
3   *