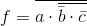Преобразование выражения только с использованием логических элементов NAND

Question

Преобразование выражения только с использованием логических элементов NAND

Как мне преобразовать это выражение НЕ (а) ИЛИ НЕ (б) И НЕ (в), используя только вентили NAND?? Я пытался это сделать, но не нашел правильного ответа.

-5

boolean-logic boolean-expression boolean-algebra demorgans-law

Источник

user5450230 21 окт '15 в 22:00

3 ответа

Другие вопросы по тегам boolean-logic boolean-expression boolean-algebra demorgans-law

user808655 21 окт '15 в 22:24 2015-10-21 22:24 · Answer 1 · 2015-10-21 22:24

Во-первых, все логические уравнения могут быть представлены вентилями NAND. Рассмотрим НЕ.... Просто свяжите два входа NAND вместе, и вы получите НЕ! NOT NAND - это AND, а OR - это два НЕ ворот, управляющих NAND! Это все довольно круто... Проведите небольшое исследование по математической логике, и вы должны найти детали различных методов преобразования.

user2115332 21 окт '15 в 22:21 2015-10-21 22:21 · Answer 2 · 2015-10-21 22:21

Вы можете применять следующие формулы шаг за шагом:

NOT(A) OR NOT(B) = A NAND B
A AND B = NOT(A NAND B)
NOT(A) = A NAND A

0

Источник

user2115332 21 окт '15 в 22:21

user6018512 18 мар '16 в 08:33 2016-03-18 08:33 · Answer 3 · 2016-03-18 08:33

Я бы предложил использовать сетки Ротта. Это графическое приложение законов Де Моргана, и оно полезно для оптимизации дизайна, используя только комбинации ворот NOR и NAND. Обычно это можно сделать очень быстро, не беспокоясь об ошибке.

Сетка каждого Ротта создается в соответствии с этими тремя принципами:

законы де Моргана соблюдаются путем переключения между ⋅ (конъюнкция) и + (дизъюнкция) и деления их на горизонтальные линии (отрицания),
вертикальные линии отделяют отдельные входы, изменяя количество входов логических вентилей,
в последней строке размещаются входные переменные либо в их простом, либо в отрицательном виде - это определяется индивидуально количеством горизонтальных линий над ними (начальная ¬ также считается).

Это заданное выражение в соответствующей сетке Ротта:

f = ¬a + ¬b ⋅ ¬c 
   --------------
       ⋅    +    
       | --------
       |    ⋅
       |    |
     a | ¬b | ¬c

Как видите, исходное выражение было преобразовано в эквивалент, то есть с использованием только двух 2-входных вентилей NAND (и некоторых инверторов, которые также могут быть заменены вентилями NAND). Сетка - это просто графическое представление применения законов Де Моргана к исходному выражению:

f =    (¬a  +  (¬b ⋅ ¬c))
  = ¬(¬(¬a  +  (¬b ⋅ ¬c)))        //double negation law: ¬(¬x) = x
  =  ¬(¬¬a  ⋅ ¬(¬b ⋅ ¬c))         //De Morgan's law
  =    ¬(a  ⋅ ¬(¬b ⋅ ¬c))         //double negation law: ¬¬a = a

f = nand(a, nand(not(b), not(c)))

(Изображение.gif было создано с использованием онлайн-инструмента для латекса)