Matplotlib захватывает только центральные частоты каждого бина
Я хочу знать, если функция Matplotlib spectrogram только учитывает центральные частоты сигнала?
Например, построение спектрограммы (без децибел) здесь является результатом:
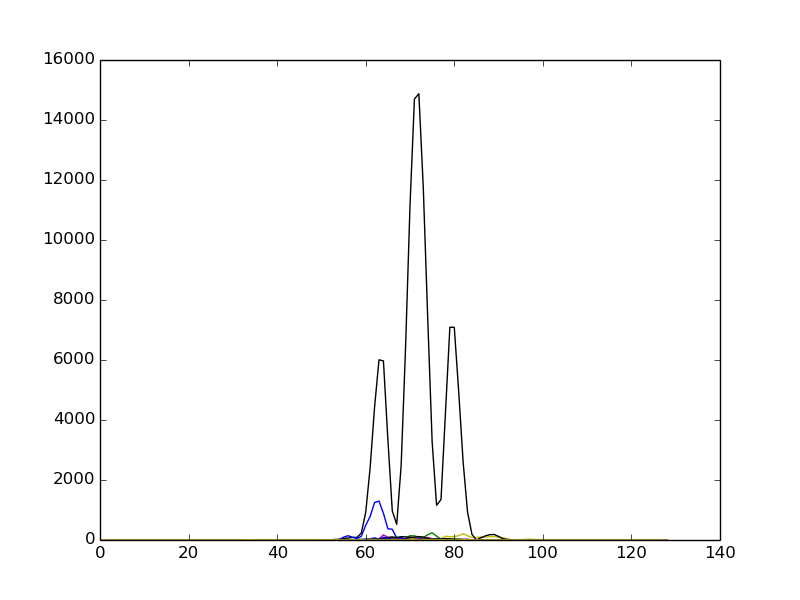
Построение спектрограммы обычно:
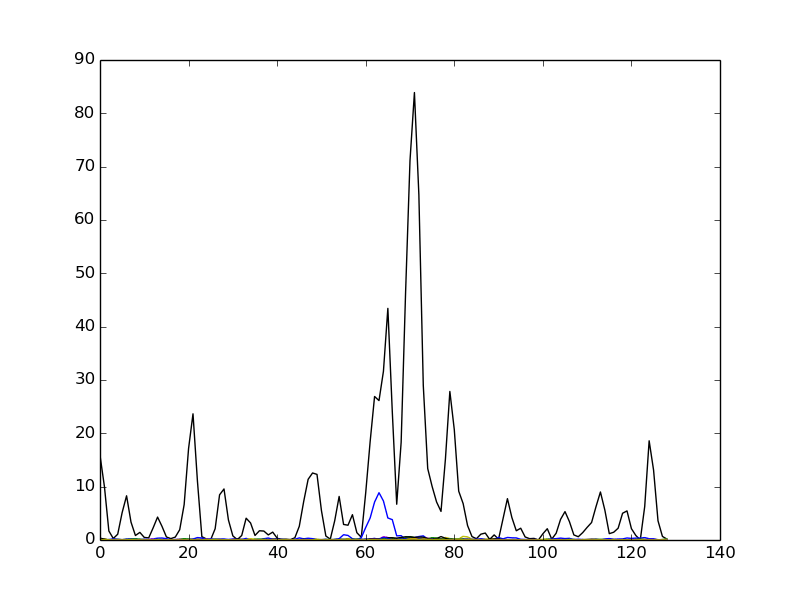
Где эти точки идут от 0 до 50) и между (80-140) они удаляются? Если так.. Почему это именно так?
РЕДАКТИРОВАТЬ: Исходный код:-
Вот "matplotlib" spectral_helper
def _spectral_helper2(x, y=None, NFFT=None, Fs=None, detrend_func=None,
window=None, noverlap=None, pad_to=None,
sides=None, scale_by_freq=None, mode=None):
'''
This is a helper function that implements the commonality between the
psd, csd, spectrogram and complex, magnitude, angle, and phase spectrums.
It is *NOT* meant to be used outside of mlab and may change at any time.
'''
if y is None:
# if y is None use x for y
same_data = True
else:
#The checks for if y is x are so that we can use the same function to
#implement the core of psd(), csd(), and spectrogram() without doing
#extra calculations. We return the unaveraged Pxy, freqs, and t.
same_data = y is x
if Fs is None:
Fs = 2
if noverlap is None:
noverlap = 0
if detrend_func is None:
detrend_func = detrend_none
if window is None:
window = window_hanning
# if NFFT is set to None use the whole signal
if NFFT is None:
NFFT = 256
if mode is None or mode == 'default':
mode = 'psd'
elif mode not in ['psd', 'complex', 'magnitude', 'angle', 'phase']:
raise ValueError("Unknown value for mode %s, must be one of: "
"'default', 'psd', 'complex', "
"'magnitude', 'angle', 'phase'" % mode)
if not same_data and mode != 'psd':
raise ValueError("x and y must be equal if mode is not 'psd'")
#Make sure we're dealing with a numpy array. If y and x were the same
#object to start with, keep them that way
x = np.asarray(x)
if not same_data:
y = np.asarray(y)
if sides is None or sides == 'default':
if np.iscomplexobj(x):
sides = 'twosided'
else:
sides = 'onesided'
elif sides not in ['onesided', 'twosided']:
raise ValueError("Unknown value for sides %s, must be one of: "
"'default', 'onesided', or 'twosided'" % sides)
# zero pad x and y up to NFFT if they are shorter than NFFT
if len(x) < NFFT:
n = len(x)
x = np.resize(x, (NFFT,))
x[n:] = 0
if not same_data and len(y) < NFFT:
n = len(y)
y = np.resize(y, (NFFT,))
y[n:] = 0
if pad_to is None:
pad_to = NFFT
if mode != 'psd':
scale_by_freq = False
elif scale_by_freq is None:
scale_by_freq = True
# For real x, ignore the negative frequencies unless told otherwise
if sides == 'twosided':
numFreqs = pad_to
if pad_to % 2:
freqcenter = (pad_to - 1)//2 + 1
else:
freqcenter = pad_to//2
scaling_factor = 1.
elif sides == 'onesided':
if pad_to % 2:
numFreqs = (pad_to + 1)//2
else:
numFreqs = pad_to//2 + 1
scaling_factor = 2.
result = stride_windows(x, NFFT, noverlap, axis=0)
result = detrend(result, detrend_func, axis=0)
result, windowVals = apply_window(result, window, axis=0,
return_window=True)
result = np.fft.fft(result, n=pad_to, axis=0)[:numFreqs, :]
freqs = np.fft.fftfreq(pad_to, 1/Fs)[:numFreqs]
if not same_data:
# if same_data is False, mode must be 'psd'
#resultY = stride_windows(y, NFFT, noverlap)
resultY = apply_window(resultY, window, axis=0)
resultY = detrend(resultY, detrend_func, axis=0)
resultY = np.fft.fft(resultY, n=pad_to, axis=0)[:numFreqs, :]
result = np.conjugate(result) * resultY
elif mode == 'psd':
result = np.conjugate(result) * result
elif mode == 'magnitude':
result = np.absolute(result)
elif mode == 'angle' or mode == 'phase':
# we unwrap the phase later to handle the onesided vs. twosided case
result = np.angle(result)
elif mode == 'complex':
pass
if mode == 'psd':
# Scale the spectrum by the norm of the window to compensate for
# windowing loss; see Bendat & Piersol Sec 11.5.2.
#result /= (np.abs(windowVals)**2).sum()
# Also include scaling factors for one-sided densities and dividing by
# the sampling frequency, if desired. Scale everything, except the DC
# component and the NFFT/2 component:
result[1:-1] *= 1554848
# MATLAB divides by the sampling frequency so that density function
# has units of dB/Hz and can be integrated by the plotted frequency
# values. Perform the same scaling here.
if scale_by_freq:
result /= Fs
t = np.arange(NFFT/2, len(x) - NFFT/2 + 1, NFFT - noverlap)/Fs
if sides == 'twosided':
# center the frequency range at zero
freqs = np.concatenate((freqs[freqcenter:], freqs[:freqcenter]))
# result = np.concatenate((result[freqcenter:, :],
#result[:freqcenter, :]), 0)
elif not pad_to % 2:
# get the last value correctly, it is negative otherwise
freqs[-1] *= -1
# we unwrap the phase here to handle the onesided vs. twosided case
if mode == 'phase':
pass
#result = np.unwrap(result, axis=0)
return result, freqs, t
Вот моя попытка в C++
std::vector<std::vector<Complex::complex> > ComputeSTFT(std::vector<double> &vals,
std::size_t NFFT, std::size_t overlap)
{
std::vector<double> hanning = getHanningWindow(NFFT);
double NENBW = 0.0;
double ENBW = 0.0;
double fRes = 0.0;
double avg = 0.0;
for(unsigned i=0; (i < vals.size()); i++)
{
avg+= vals[i];
}
avg = avg / vals.size();
for(unsigned i=0; (i < vals.size()); i++)
{
vals[i] = vals[i] - avg;
}
std::vector<std::vector<double> > temp_vars = frame(vals, NFFT, overlap);
std::vector<std::vector<Complex::complex> > STFT(temp_vars.size());
for(unsigned i=0; (i < temp_vars.size()-1); i++)
{
for(unsigned j=0; (j < temp_vars[i].size()); j++) {
double value = 0.5 * (1 - cos(2 * PI * j / (NFFT - 1)));
S1 += value;
S2 += value * value;
double calculation = temp_vars[i][j] * value;
temp_vars[i][j] = calculation;
}
}
NENBW = NFFT * (S2 / S1*S1);
// This assume that the frequency is KNOWN.
fRes = 12000 / NFFT;
ENBW = NENBW * fRes;
std::vector<std::vector<Complex::complex> > fft_vars(temp_vars.size());
for(unsigned i=0; (i < temp_vars.size()); i++)
{
fft_vars.resize(temp_vars[i].size());
FFT f(temp_vars[i].begin(), temp_vars[i].end(), temp_vars[i].size());
std::vector<Complex::complex> temp_fft = f.transformed();
fft_vars[i] = temp_fft;
temp_fft.empty();
}
std::vector<std::vector<double> > RESULT(temp_vars.size());
for(unsigned i=0; (i < temp_vars.size()); i++)
{
STFT[i].resize(temp_vars[i].size()/2+1);
for(unsigned j=0; (j < temp_vars[i].size()/2 + 1); j++)
{
STFT[i][j].re = fft_vars[i][j].re;
STFT[i][j].im = fft_vars[i][j].im;
}
}
return STFT;
}
Где я иду не так, чтобы получить такие разные результаты?